数组和广义表

数组

• 数组是一种存储结构，是很多语言内建的数据类型。它的操作只有按下标读写。
• 数组是一种逻辑结构。
  • 一维数组属于线性结构，但是不是线性表，因为数组中的元素虽然在存储结构上连续，但是在逻辑结构上不一定连续：即数组可以是稀疏的，也不需要顺序存取。一维数组被称为向量。
  • 一维数组的元素属于不可分割的原子元素是时，是线性结构。
  • 当它的元素为数组时，即多维数组时，是非线性结构。

一维数组

下标从 $0$ 开始，到 $n-1$ 结束，共有 $n$ 个元素。

$$LOC(a[i])=LOC(a[0])+i\times \text{sizeof}(a[0])$$

多维数组

二维数组

二维数组 $a[m][n]$ 的存储结构， $m$ 行 $n$ 列：

• 行优先存储：$$LOC(a[i][j])=LOC(a[0][0])+(i\times n+j)\times \text{sizeof}(a[0][0])$$
• 列优先存储：$$LOC(a[i][j])=LOC(a[0][0])+(j\times m+i)\times \text{sizeof}(a[0][0])$$

多维数组

多维数组 $a[m_1][m_2][\cdots ][m_k]$ 的存储结构：

• 行优先存储：$$LOC(a[i_1][i_2][\cdots ][i_k])=LOC(a[0][0][\cdots ][0])+(\sum _{j=1}^k\left(\prod _{l=j+1}^k{m}_l\right)\times i_j)\times \text{sizeof}(a[0][0][\cdots ][0])$$
• 列优先存储：$$LOC(a[i_1][i_2][\cdots ][i_k])=LOC(a[0][0][\cdots ][0])+(\sum _{j=1}^k\left(\prod _{l=1}^{j-1}{m}_l\right)\times i_j)\times \text{sizeof}(a[0][0][\cdots ][0])$$

压缩矩阵

对称矩阵行优先压缩存储上三角矩阵

用一维数组存储对称矩阵 $a[n][n]$ 的元素，只存储主对角线及其上方的元素。 顺序是 a[0][0]、a[0][1]、a[0][2]、$\cdots$、a[0][n-1]、a[1][1]、a[1][2]、$\cdots$、a[1][n-1]、$\cdots$、a[n-1][n-1]。

$$LOC(a[i][j])=\{\begin{array}{ll}LOC(a[0][0])+\frac{(n+n-i-1)\times i}{2}+j-i& i\le j\\ LOC(a[0][0])+\frac{(n+n-j-1)\times j}{2}+i-j& i>j\end{array}$$

对称矩阵列优先压缩存储下三角矩阵

用一维数组存储对称矩阵 $a[n][n]$ 的元素，只存储主对角线及其下方的元素。 顺序是 a[0][0]、a[1][0]、a[1][1]、a[2][0]、a[2][1]、a[2][2]、$\cdots$、a[n-1][0]、a[n-1][1]、$\cdots$、a[n-1][n-1]。

$$LOC(a[i][j])=\{\begin{array}{ll}LOC(a[0][0])+\frac{i\times (i+1)}{2}+j& i\ge j\\ LOC(a[0][0])+\frac{j\times (j+1)}{2}+i& i<j\end{array}$$

三对角矩阵

用一维数组存储三对角矩阵 $a[n][n]$ 的元素，只存储主对角线及其上下相邻的两条对角线的元素。 顺序是 a[0][0]、a[0][1]、a[1][0]、a[1][1]、a[1][2]、a[2][1]、a[2][2]、$\cdots$、a[n-2][n-2]、a[n-2][n-1]、a[n-1][n-2]、a[n-1][n-1]。

主要讨论行优先存储的情况：

从矩阵到一维数组

$$LOC(a[i][j])=(3\times i-1)+(j-i+1)=2timesi+j$$

从一维数组到矩阵

$$\begin{array}{rl}i& =\lfloor \frac{k+1}{3}\rfloor \\ j& =k-2\times i\end{array}$$

稀疏矩阵

设在一个 $m$ 行 $n$ 列的矩阵中，有 $t$ 个非零元素，定义稀疏因子：

$$\delta =\frac{t}{m\times n}$$

通常当这个值小于 $0.05$ 时，称为稀疏矩阵。

三元组表

采用三元组 $(i,j,e)$ 表示矩阵中的非零元素，其中 $i$ 为行号，$j$ 为列号，$e$ 为元素值。 在数组中按照行优先存储，即先存储第一行的元素，再存储第二行的元素，以此类推。

矩阵转置

void fastTransposeSMatrix(SparseMatrix& a, SparseMatrix& b)
{
    if (a.terms <= 0) return;

    b.rows = a.cols;
    b.cols = a.rows;
    b.terms = a.terms;

    int rowSize = new int[a.cols];  // 记录转置后每一行的非零元素个数
    int rowStart = new int[a.cols];  // 在存储转置的过程中，该行该放在三元组表的哪个位置

    for (int i = 0; i < a.term; ++i)
        ++rowSize[a.data[i].col];

    for (int i = 1; i < a.cols; ++i)
        rowStart[i] = rowStart[i - 1] + rowSize[i - 1]; // 类似于计数排序

    for (int i = 0; i < a.term; ++i)
    {
        int j = rowStart[a.data[i].col];

        b.data[j].row = a.data[i].col;
        b.data[j].col = a.data[i].row;
        b.data[j].value = a.data[i].value;

        ++rowStart[a.data[i].col];
    }

    delete[] rowSize;
    delete[] rowStart;
}

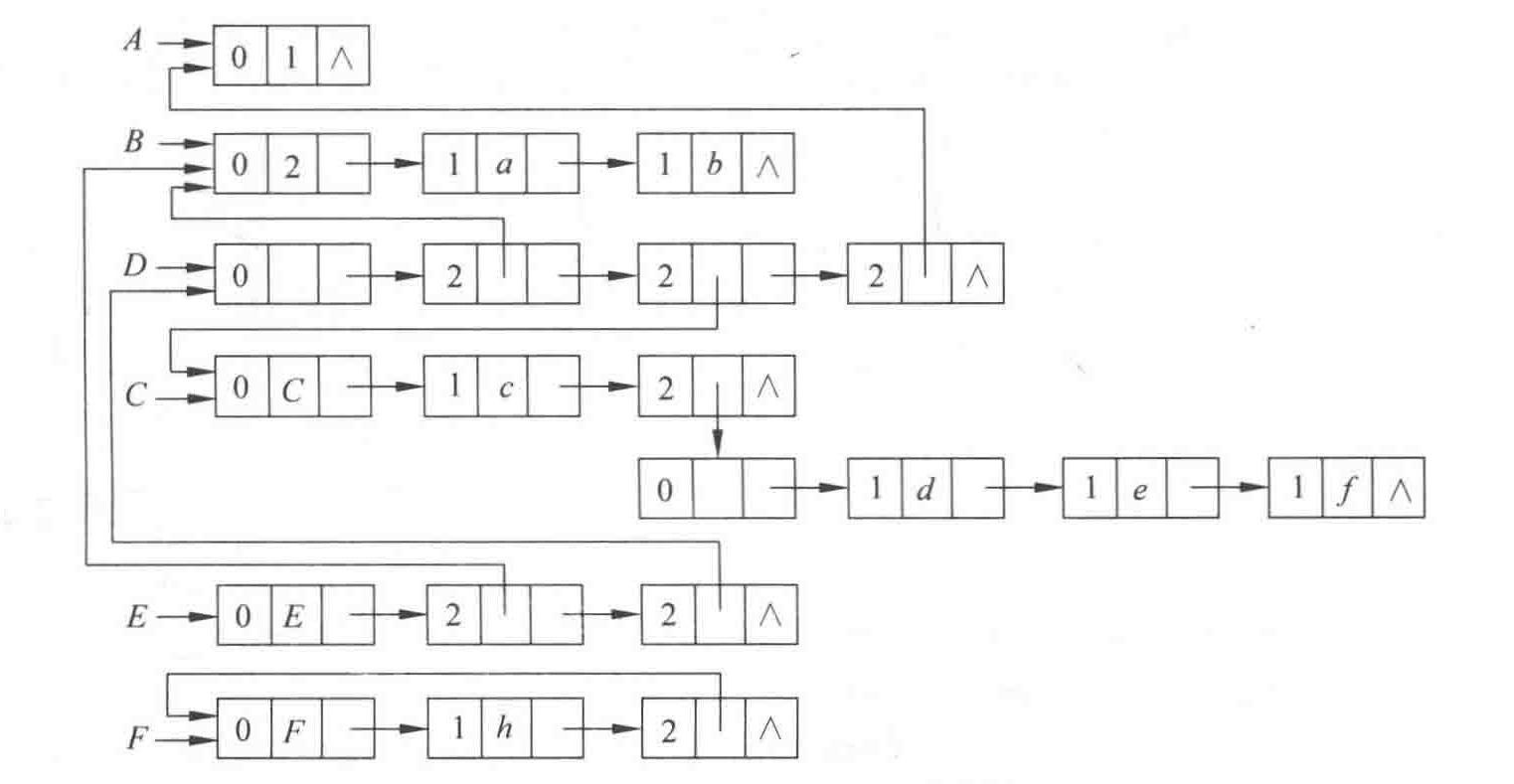
链表表示

用链表表示稀疏矩阵，可以在运算的过程中有效地动态调整矩阵的大小。

简单链式存储

链表的每个结点是一个四元组 $(i,j,e,\text{next})$

虽然有利于插入和删除操作，但是失去了矩阵的灵活性。

行链表组

每一行用一个链表表示，链表的每个结点是一个三元组 $(j,e,\text{next})$ 共有 $m$ 个头指针，指针域指向每一行的第一个非零元素。

十字链表

每个非零元素是一个六元组 $(head,i,j,down,value,right)$ 分别记录了是否为头指针、行号、列号、在下面的第一个非零元素、元素值、在右边的第一个非零元素。

行和列共享同一个头指针结点， $right$ 表示的是第 $i$ 行的 第一个非零元素， $down$ 表示的是第 $i$ 列的第一个非零元素。

广义表

$$LS=({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)$$$${\alpha }_i=\{\begin{array}{ll}(a_1,a_2,\cdots ,a_m)& \text{广义表}\\ e& \text{原子元素}\end{array}$$

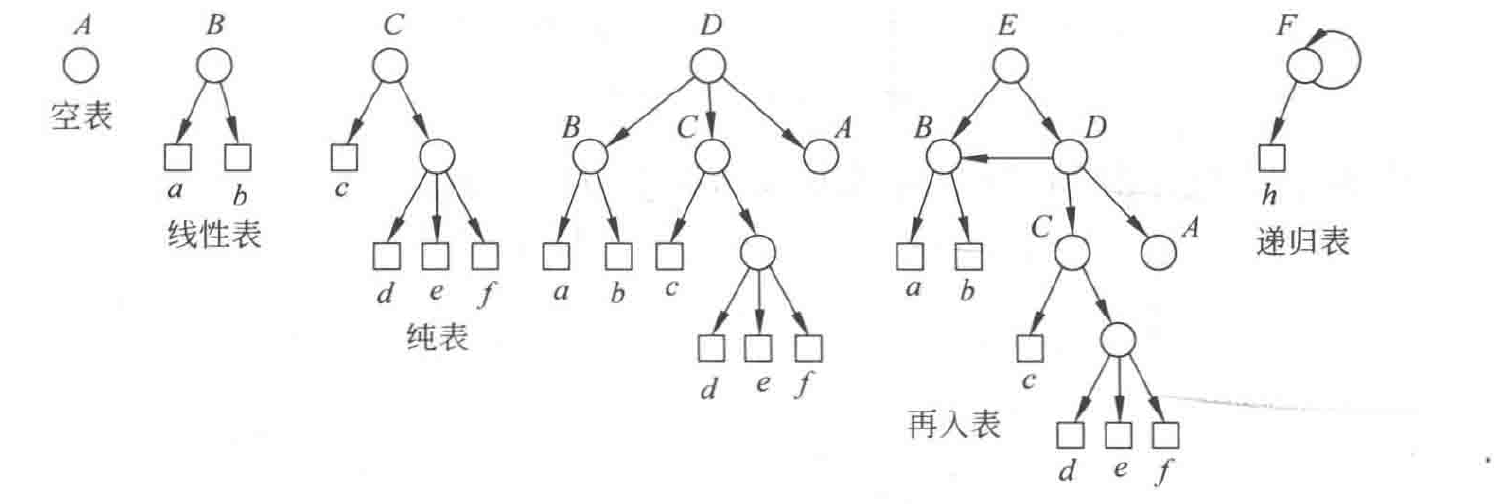
广义表的定义是 递归 的。 当每个元素均为原子元素且类型相同时，广义表即为线性表。

• 表头：第一个元素，是一个原子元素或者广义表。
• 表尾：除去表头之外的部分，是一个广义表。
• 表长：广义表中最外层的元素个数。
• 深度：广义表中括号 最深 的层数。原子元素的深度为 $0$，$()$ 的深度为 $1$。

广义表的性质

• 有次序性：广义表中元素之间有次序关系。
• 有长度：广义表中元素的个数称为广义表的长度。
• 有深度：广义表中元素的嵌套层数称为广义表的深度。
• 可递归：广义表本身可以是自己的子表。
• 可共享：广义表可以被其他子表共享。

广义表的链接表示

头尾表示

广义表 = 表头 + 表尾

• tag：标志域，表示当前元素是原子元素还是广义表。
• value：值域，存储原子元素的值。
• hlink，tlink：指针域，分别指向表头和表尾。

每个指针指向的都是一个广义表的头结点，即先在剩下的元素外面加上一层括号。

扩展的线性链表

和头尾表示类似，只不过原子元素也存储了 tlink 指针。 扩展的线性链表的指针直接指向下一个元素，而不是指向广义表的头结点。

层次链表

结合了上述两种表示方法，拥有头指针以及指向下一个元素的指针。