计算模型

问题与决定性问题

判定性问题

只需要回答"是"或"否"的问题。

如：

1. 一个图是否连通？
2. 一个数是否是素数？

功能性问题

需要给出一个解决方案的问题。 如 排序，最大流，最大团等等。

本课程只讨论判定性问题。

有限自动机与正则语言

有限自动机是一个五元组$(Q,\mathrm{\Sigma },\delta ,q_0,F)$，其中：

1. $Q$ 是有限集，称为状态集。
2. $\mathrm{\Sigma }$ 是有限集，称为字母表。
3. $\delta$ 是转移函数。
4. $q_0\in Q$ 是初始状态。
5. $F\subseteq Q$ 是接受状态。

有限自动机计算的形式定义

设 $M=(Q,\mathrm{\Sigma },\delta ,q_0,F)$ 是一个有限自动机，$w=w_1{w}_2\cdots w_n$ 是一个字符串，其中 $w_i\in \mathrm{\Sigma }$。

若存在 $Q$ 的一个状态序列 $r_0,r_1,\cdots ,r_n$，使得：

1. $r_0=q_0$。
2. $r_{i+1}=\delta (r_i,w_{i+1})$，对 $i=0,1,\cdots ,n-1$。
3. $r_n\in F$。

则称 $M$ 接受字符串 $w$。 记为 $\delta (r_0,w)\in F$。

识别语言

对于一个有限自动机 $M$，若 $A=\{w\in {\mathrm{\Sigma }}^{\ast }|\delta (q_0,w)\in F\}$，则称 $A$ 是 $M$ 的语言，记为 $L(M)=A$，也称 $M$ 识别 $A$。

$M$ 识别的语言唯一，不识别任意其他语言。

正则语言

若存在一个有限自动机 $M$，使得 $L(M)=A$，则称 $A$ 是一个正则语言。

等价

若两个有限自动机的语言相同，则称它们是等价的。

正则运算

1. 并：$A\cup B=\{w|w\in A\text{ 或 }w\in B\}$。
2. 连接：$A\circ B=\{w|w=w_1{w}_2,w_1\in A,w_2\in B\}$。
3. 星号：$A^{\ast }=A^0\cup A^1\cup A^2\cup \cdots$，其中 $A^0=\{\epsilon \}$，$A^1=A$，$A^2=A\circ A$。 即 $A^{\ast }=\{w_1{w}_2\cdots w_n|n\ge 0,w_i\in A\}$。
4. 补：$A^c={\mathrm{\Sigma }}^{\ast }-A$。

正则语言对这四种运算封闭。 则相对补与对称差运算也是封闭的。 即 $A-B=A\cap B^c$，$A\oplus B=(A-B)\cup (B-A)$。

非确定性

当机器处于给定的状态并读入下一个输入符号时，可以知道机器的下一个状态是什么——它是确定的。因此，称这是确定型计算 $(\mathrm{deterministic}\mathrm{computation})$。在非确定型$(\mathrm{nondeterministic})$机器中，在任何一点，下一个状态可能存在若干个选择。

确定型有限自动机：$(\mathrm{Deterministic}\mathrm{Finite}\mathrm{Automaton},\mathrm{DFA})$非确定型有限自动机：$(\mathrm{Nondeterministic}\mathrm{Finite}\mathrm{Automaton},\mathrm{NFA})$

非确定性是确定性的推广，因此每一台 $\mathrm{DFA}$ 自动地是一台 $\mathrm{NFA}$ 。

确定型有限自动机 (DFA)

$\delta :Q\times \mathrm{\Sigma }\to Q$ 是一个函数，对于每一个 $q\in Q$ 和 $\sigma \in \mathrm{\Sigma }$，$\delta (q,\sigma )$ 是唯一的。

非确定型有限自动机 (NFA)

$\delta :Q\times {\mathrm{\Sigma }}_{\epsilon }\to P(Q)$ 是一个函数，对于每一个 $q\in Q$ 和 $\sigma \in {\mathrm{\Sigma }}_{\epsilon }$，$\delta (q,\sigma )$ 是一个状态集合，可能进入多个状态。

转移箭头函数上的符号可以是 $\epsilon$，表示可以不读入任何输入就转移。

NFA的计算方式

1. 若读到输入字符 $s$，机器把自己备份 $0$ 次或多次，然后从这些备份中选择一个状态，继续读入下一个字符。
2. 若读到 $\epsilon$，机器将自己备份一次，然后继续读入下一个字符。
3. 读入下一个输入符号，若该符号存在于备份状态的转移函数中，则转 $1$，否则停机。
4. 机器检查是否有一个备份状态是接受状态。若存在一个副本是接受状态，则接受输入。

对于输入，$\mathrm{NFA}$ 计算的路径可能不唯一。

NFA 与 DFA 等价

对于每一个 $\mathrm{NFA}$，都存在一个等价的 $\mathrm{DFA}$。

子集构造法

$\mathrm{NFA}$：$\mathrm{N}=(Q,\mathrm{\Sigma },\delta ,q_0,F)$$\mathrm{DFA}$：$\mathrm{M}=(Q^{\prime },\mathrm{\Sigma },{\delta }^{\prime },q_0^{\prime },F^{\prime })$

1. $Q^{\prime }=2^Q$，即 $\mathrm{DFA}$ 的状态集是 $\mathrm{NFA}$ 的状态集的幂集。
2. $E$ 表示 $\epsilon$ 闭包，即 $E(S)=\{q|q\in S\text{ 或 }q\text{ 可以通过若干个 }\epsilon \text{ 转移到 }S\}$。
3. $q_0^{\prime }=E(\{q_0\})$。
4. ${\delta }^{\prime }(S,a)=E(\bigcup _{q\in S}\delta (q,a))$，其中 $S\in Q^{\prime }$，$a\in \mathrm{\Sigma }$。
5. $F^{\prime }=\{S\in Q^{\prime }|S\cap F\ne \varnothing \}$。

正则表达式

若 $R$ 是一个正则表达式，则 $R$ 是

1. $a,a\in \mathrm{\Sigma }$。
2. $\epsilon$。
3. $\varnothing$。
4. $(R_1\cup R_2)$, $R_1$ 和 $R_2$ 是正则表达式。
5. $(R_1\circ R_2)$, $R_1$ 和 $R_2$ 是正则表达式。
6. $(R_1^{\ast })$，$R_1$ 是正则表达式。

每个正则表达式 $R$ 表示一种正则语言 $L(R)$。

1. $L(a)=\{a\}$。
2. $L(\epsilon )=\{\epsilon \}$。
3. $L(\varnothing )=\varnothing$。
4. $L(R_1\cup R_2)=L(R_1)\cup L(R_2)$。
5. $L(R_1\circ R_2)=L(R_1)\circ L(R_2)$。
6. $L(R_1^{\ast })=(L(R_1){)}^{\ast }$。

正则表达式与有限自动机等价

－个语言是正则的，当且仅当可以用正则表达式描述它。

由正则表达式构造有限自动机

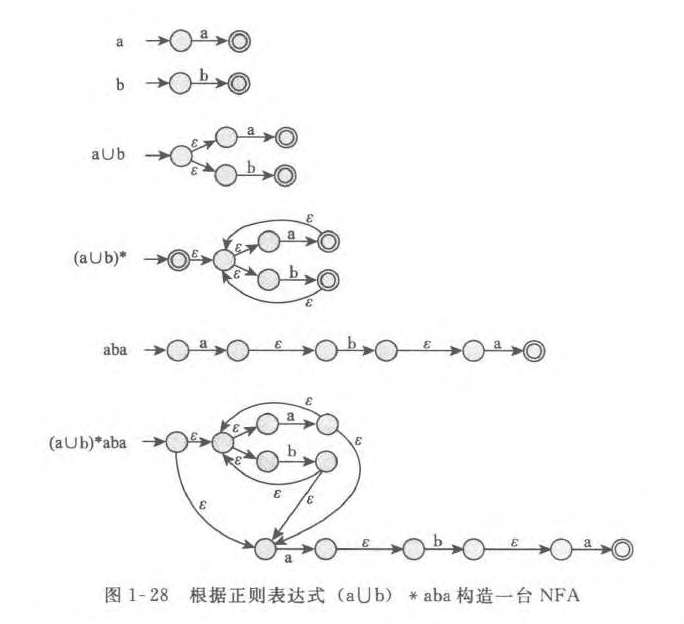
由有限自动机构造正则表达式

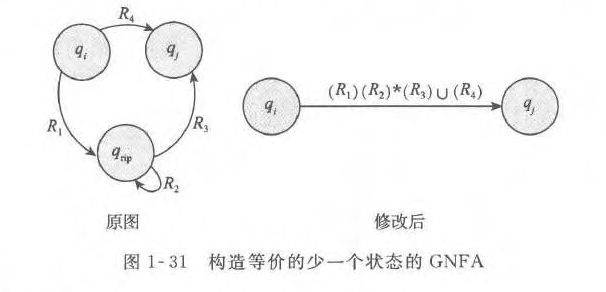
泵引理

若 $A$ 是一个正则语言，则存在一个整数 $p$，使得对于任意 $w\in A$，若 $|w|\ge p$，则 $w$ 可以被分解为 $w=xyz$，满足：

1. 对于任意 $i\ge 0$，$x{y}^{i}z\in A$。
2. $|y|>0$。
3. $|xy|\le p$。

图灵机

图灵机 $(\mathrm{Turing}\mathrm{Machine},\mathrm{TM})$ 是一个七元组 $(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,q_{\text{accept}},q_{\text{reject}})$，其中：

1. $Q$ 是有限集，称为状态集。
2. $\mathrm{\Sigma }$ 是有限集，称为输入字母表，不包含特殊空白符号 $\bigsqcup$。
3. $\mathrm{\Gamma }$ 是有限集，称为带子字母表，$\mathrm{\Sigma }\subseteq \mathrm{\Gamma }$，且 $\bigsqcup \in \mathrm{\Gamma }-\mathrm{\Sigma }$。
4. $\delta :Q\times \mathrm{\Gamma }\to Q\times \mathrm{\Gamma }\times \{L,R\}$ 是转移函数。即 $\delta (q,a)=(r,b,L/R)$ 表示在状态 $q$ 读入字符 $a$ 后，将字符 $a$ 替换为字符 $b$，转移到状态 $r$，第三个参数 $L/R$ 表示下一步向左 / 向右移动。
5. $q_0\in Q$ 是初始状态。
6. $q_{\text{accept}}\in Q$ 是接受状态。
7. $q_{\text{reject}}\in Q$ 是拒绝状态，且 $q_{\text{reject}}\ne q_{\text{accept}}$。

图灵机的初始化

设 $M=(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,q_{\text{accept}},q_{\text{reject}})$ 是一个图灵机，$w=w_1{w}_2\cdots w_n$ 是一个字符串，其中 $w_i\in \mathrm{\Sigma }$。

1. 输入带：将 $w$ 放在最左端，其余位置填充 $\bigsqcup$。
2. 状态：初始状态为 $q_0$。
3. 读写头：指向第一个字符 $w_1$。

图灵机的格局

对于一个图灵机 $M=(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,q_{\text{accept}},q_{\text{reject}})$，设 $q\in Q$ ， $u,v\in {\mathrm{\Gamma }}^{\ast }$， 则 格局 $uqv$ 表示：

1. 状态：$q$。
2. 存储带：存储带上的内容为 $uv$，其余为空白符号 $\bigsqcup$。
3. 读写头：指向 $v$ 的第一个字符。

格局的分类

• 起始格局：$q_{0}w$。
• 接受格局：$u{q}_{\text{accept}}v$。
• 拒绝格局：$u{q}_{\text{reject}}v$。
• 停机格局：$uqv$，其中 $q\in \{q_{\text{accept}},q_{\text{reject}}\}$。

格局的转移

• 如果 $\delta (q_i,b)=(q_j,c,L)$，则
  • $ua{q}_{i}bv\to u{q}_{j}acv$
  • $q_{i}bv\to q_{j}cv$
• 如果 $\delta (q_i,b)=(q_j,c,R)$，则
  • $ua{q}_{i}bv\to uac{q}_{j}v$

图灵机的计算

设 $M=(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,q_{\text{accept}},q_{\text{reject}})$ 是一个图灵机，$w=w_1{w}_2\cdots w_n$ 是一个字符串，其中 $w_i\in \mathrm{\Sigma }$。

若存在格局序列 $C_1,C_2,\cdots ,C_k$，使得

1. $C_1=q_{0}w$。
2. 对于 $i=1,2,\cdots ,k-1$，$C_i\to C_{i+1}$。
3. $C_k$ 是停机格局。

则称 $M$ 接受字符串 $w$。

图灵机 $M$ 接受 的所有字符串的集合称为 $M$ 接受 / 识别 的语言，记为 $L(M)$。

图灵机运行的结果

• 若 $\mathrm{TM}$ 进入接受状态，则停机且接受输入。
• 若 $\mathrm{TM}$ 进入拒绝状态，则停机且拒绝输入。
• 否则，$\mathrm{TM}$ 一直运行，不停机。

若图灵机 $M$ 对所有输入都停机，则称 $M$ 是判定器。
即对于任意输入，$M$ 要么接受，要么拒绝，不会无限循环。

对于可以识别某个语言的判定器 $M$，称 $M$ 判定该语言。

语言的分类

• 图灵可识别语言：存在一个图灵机可以识别该语言。

  • 也称递归可枚举语言。
    • = 递归可枚举
    • = 计算可枚举
    • = 半可判定
    • = 半可计算

• 图灵可判定语言：存在一个图灵机可以判定该语言。

  • 也称递归语言。
    • = 递归
    • = 可解
    • = 可行
    • = 可判定
    • = 可计算

包含关系：

graph TD
    subgraph turing_recognizable["图灵可识别语言"]
        subgraph turing_decidable["图灵可判定语言"]
            regex_language["正则语言"]
        end
    end
    classDef circleStyle fill:#dd1,color:black,stroke:#333,stroke-width:4px;

    class turing_recognizable circleStyle;
    class turing_decidable circleStyle;
    class regex_language circleStyle;

图灵机的描述

1. 形式水平的描述：状态图或转移函数
2. 实现水平的描述：读写头的移动与读写，状态的转移
3. 高水平的描述：使用日常语言描述 例如

$M$ = "对于输入串 $w$

1. 若 $w$ = $ϵ$，则接受
2. 若只有一个 $0$，则接受
3. 若 $0$ 的个数是奇数，则拒绝
4. 从带左端隔一个 $0$ 删除一个 $0$，转移到步骤 $2$"

由定义，图灵机的输入总是字符串。
有时候要输入数，图，或图灵机等对象，要将对象编码成字符串。
记对象 O 的编码为 <O>。

特别的，图灵机是有向带权图也可以编码为字符串。

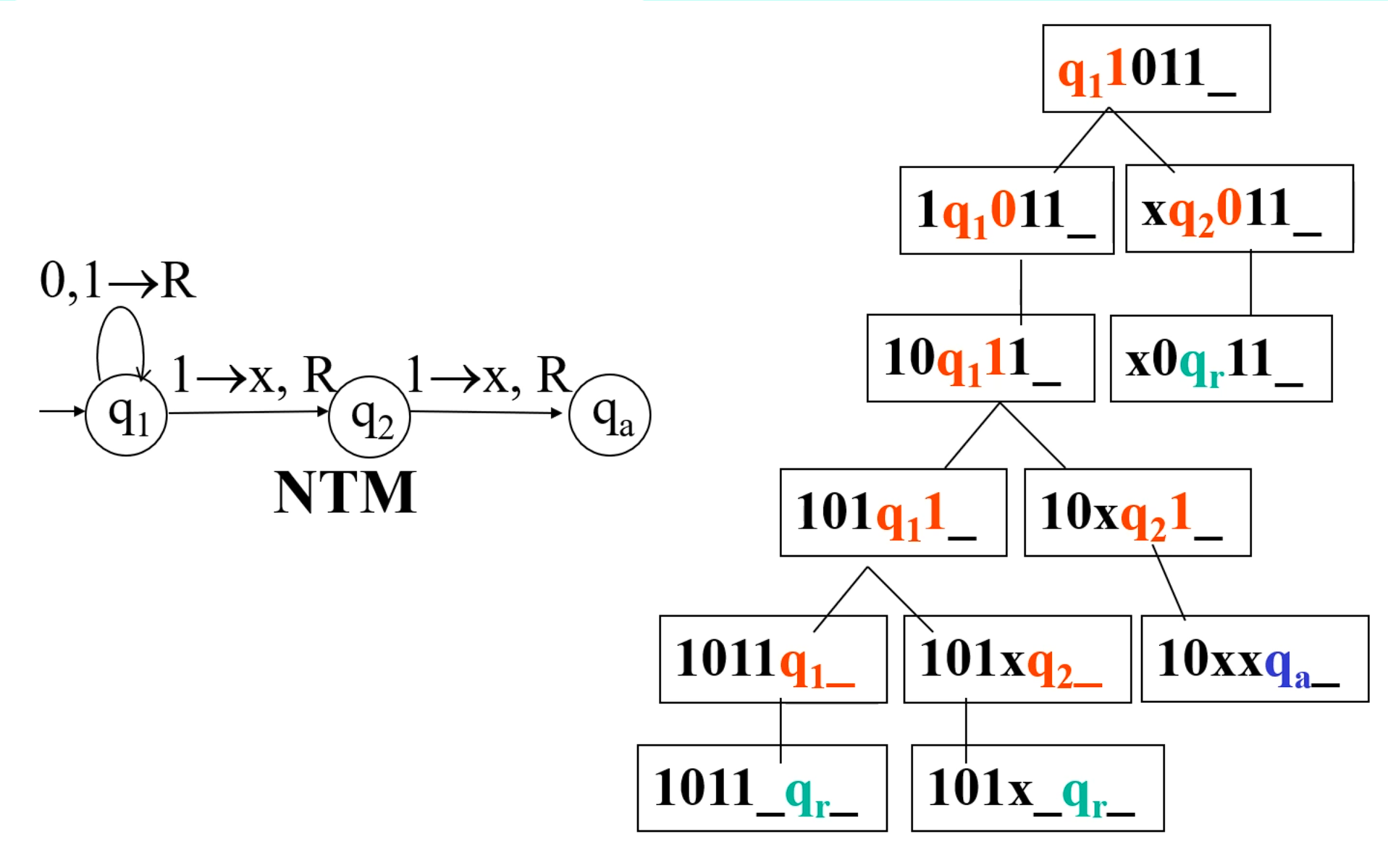
非确定性图灵机

非确定性图灵机 $(\mathrm{Nondeterministic}\mathrm{Turing}\mathrm{Machine},\mathrm{NTM})$ 是一个七元组 $(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,q_{\text{accept}},q_{\text{reject}})$，它的转移函数是 $\delta :Q\times \mathrm{\Gamma }\to P(Q\times \mathrm{\Gamma }\times \{L,R\})$。

如果计算的某个分支导致接受状态，则机器接受该输入。

称 $\mathrm{NTM}$ $M$接受 $x$ ， 若在 $x$ 上运行 $M$ 时有接受分支。
称一个 $\mathrm{NTM}$ 为判定的，若它对所有输入，所有分支都停机。

每个 $\mathrm{NTM}$ 都有等价的 $\mathrm{DTM}$
每个判定 $\mathrm{NTM}$ 都有等价的判定 $\mathrm{DTM}$

图灵可识别当且仅当可用非确定型图灵机识别。
图灵可判定当且仅当可用非确定型图灵机判定。