毕奥-萨伐尔定律

真空中电流元产生的磁感应强度为：

$$d\mathit{B}=\frac{{\mu }_0}{4\pi }\frac{Id\mathit{l}\times {\mathit{e}}_{\mathit{r}}}{r^2}$$

其中， ${\mu }_0$ 为 真空磁导率，其值为 $4\pi \times {10}^{-7}\text{T}\cdot \text{m}/\text{A}$。

则 $d\mathit{B}$ 的大小为

$$dB=\frac{{\mu }_0}{4\pi }\frac{Idl\sin \theta }{r^2}$$

其中， $\theta$ 为 $d\mathit{l}$ 与 ${\mathit{e}}_{\mathit{r}}$ 的夹角。

因此电流元产生的磁场与电流元的大小成正比，与距离的平方成反比。
和库仑定律一样满足反比平方定律。 方向由右手螺旋定则确定。

毕奥-萨伐尔定律的应用

直导线

在真空中有一段长为 $L$ 的直导线，电流为 $I$。 场点 $P$ 到直导线的垂直距离为 $a$，两端与电流方向的夹角分别为 ${\theta }_1$ 和 ${\theta }_2$。

$$B=\int dB=\frac{{\mu }_0}{4\pi }I\int \frac{dl\sin \theta }{r^2}$$

其中 $r$ = $\frac{a}{\sin \theta }$，$l=-a\cot \theta$，则 $dl=\frac{a}{{\sin }^2\theta }d\theta$。 将 $l$ 和 $dl$ 代入上式，得

$$\begin{array}{rl}sB& =\frac{{\mu }_0}{4\pi }I{\int }_{{\theta }_1}^{{\theta }_2}\frac{\sin \theta }{a^2/{\sin }^2\theta }\frac{a}{{\sin }^2\theta }d\theta \\ & =\frac{{\mu }_0}{4\pi a}I{\int }_{{\theta }_1}^{{\theta }_2}d\theta =\frac{{\mu }_0}{4\pi a}I(\cos {\theta }_1-\cos {\theta }_2)\end{array}$$

1. 无限长直导线
   • ${\theta }_1=0$
   • ${\theta }_2=\pi$
   • $B=\frac{{\mu }_0}{2\pi a}I$
2. 半无限长直导线
   • ${\theta }_1=\frac{\pi }{2}$
   • ${\theta }_2=\pi$
   • $B=\frac{{\mu }_0}{4\pi a}I$
3. 导线延长线上的磁场
   • ${\theta }_1={\theta }_2=\pi$
   • $B=0$

载流圆线圈轴线上的磁场

在真空中有一半径为 $R$，载流量为 $I$ 的圆线圈，场点 $P$ 在圆线圈轴线上，到圆线圈中心的距离为 $x$。

$$dB=\frac{{\mu }_0}{4\pi }\frac{Idl}{r^2}$$

有

$$d{B}_{\parallel }=dB\sin \theta$$$$d{B}_{\perp }=dB\cos \theta$$

由于对称性，$d{B}_{\perp }$ 的积分为零，只需计算 $d{B}_{\parallel }$ 的积分。

$$B=\int d{B}_{\parallel }=\frac{{\mu }_0}{4\pi }I\int \frac{dl\sin \theta }{r^2}$$

式中 $\sin \theta =\frac{R}{r}$

$$B=\frac{{\mu }_{0}IR}{4\pi r^3}{\int }_0^{2\pi R}dl=\frac{{\mu }_{0}I{R}^2}{2r^3}$$

由于 $r^2=R^2+x^2$，则

$$B=\frac{{\mu }_{0}I{R}^2}{2(R^2+x^2{)}^{3/2}}$$

方向满足右手螺旋定则关系。

1. 若 $x=0$，即场点在圆线圈中心，则 $B=\frac{{\mu }_{0}I}{2R}$
2. 若载流导线为一段圆弧，则在其圆心处产生的磁场 $B=\frac{{\mu }_{0}I}{2R}\frac{\theta }{2\pi }$
3. 若 $x\gg R$，则 $B=\frac{{\mu }_{0}I{R}^2}{2x^3}$

磁偶极子

定义圆电流的磁矩为

$$\mathit{m}=I\mathit{S}$$

单位为 $\text{A}\cdot {\text{m}}^2$。

由于 $S=\pi R^2$，结合载流圆线圈轴线上的磁场公式，得

$$\mathit{B}=\frac{{\mu }_0\mathit{m}}{2\pi x^3}$$

该式与静电场中的电偶极子的电场强度表达式相似，而且磁感应线分布也与电偶极子的电场线分布相似，因此我们将圆电流称为磁偶极子。

载流直螺线管轴线上的磁场

可以视作无限多个载流圆线圈的叠加 设 $P$ 为轴线上一点，到螺线管一端的距离为 $x$，螺线管的半径为 $R$，载流量为 $I$，单位长度上有 $n$ 匝

$$dB=\frac{{\mu }_0}{2}\frac{R^{2}dI}{(R^2+x^2{)}^{3/2}}=\frac{{\mu }_0}{2}\frac{R^{2}nIdx}{(R^2+x^2{)}^{3/2}}$$$$B=\int dB=\int \frac{{\mu }_0}{2}\frac{R^{2}nIdx}{(R^2+x^2{)}^{3/2}}$$

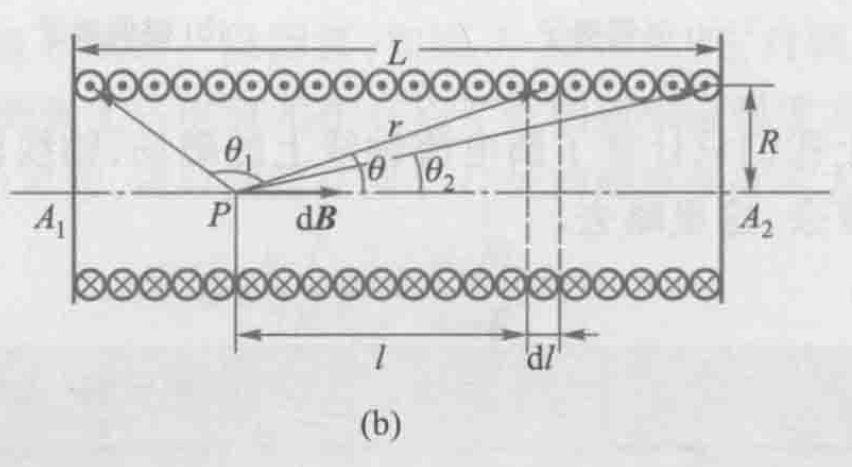
到螺线管某个微分点的距离为 $r$，夹角为 $\theta$
根据几何关系知：

$$r^2=R^2+x^2,r\sin \theta =R,x=\frac{R}{\tan \theta },dx=\frac{Rd\theta }{{\sin }^2\theta }$$

代入上式，得

$$dB=\frac{{\mu }_0}{2}\frac{R^{2}nI}{(R/\sin \theta {)}^3}\frac{Rd\theta }{{\sin }^2\theta }=\frac{{\mu }_0}{2}nI\sin \theta d\theta$$

故得 $P$ 点的磁场为

$$B=\frac{{\mu }_0}{2}nI{\int }_{{\theta }_1}^{{\theta }_2}\sin \theta d\theta =\frac{{\mu }_0}{2}nI(\cos {\theta }_1-\cos {\theta }_2)$$

1. 当 $L\gg R$ 时，螺线管近似为无限长，即 ${\theta }_1=\pi$，${\theta }_2=0$，则 $B={\mu }_{0}nI$
2. 若 $P$ 点在任意一端的中心口处，且 $L\gg R$，则有 ${\theta }_1=\pi /2$， ${\theta }_2=0$ 或 ${\theta }_1=\pi$， ${\theta }_2=\pi /2$，则 $B=\frac{{\mu }_0}{2}nI$

可见半无限长螺线管的磁场强度是无限长螺线管磁场强度的一半。