格与布尔代数

设 $⟨S,\preccurlyeq ⟩$ 是一个偏序集，若 $\mathrm{\forall }a,b\in S$，存在上确界和下确界，则称 $⟨S,\preccurlyeq ⟩$ 是一个格。

保联与保交

把求 $\{x,y\}$ 的上确界和下确界看作 $x$ 和 $y$ 的二元运算 $\vee$ 和 $\wedge$，称为保联和保交。

通常把在偏序关系的基础上定义的格称为偏序格。

实例

正因子格

$n$ 是正整数，$S_n$ 是 $n$ 的所有正因子的集合，$S_n$ 关于整除关系 $D$ 构格，称为正因子格。

• $x\vee y=\mathrm{lcm}(x,y)$
• $x\wedge y=gcd(x,y)$

幂集格

$⟨P(B),\subseteq ⟩$ 是一个格，称为幂集格。

• $A\vee B=A\cup B$
• $A\wedge B=A\cap B$

整数集

$⟨\mathbb{Z},\le ⟩$ 是一个格。

• $a\vee b=max(a,b)$
• $a\wedge b=min(a,b)$

子群格

子群格是一个格。

$$L(G)=\{H|H\le G\}$$

对任意的 $H_1,H_2\in L(G)$，$H_1\cap H_2$ 是 $G$ 的子群，$⟨H_1\cup H_2⟩$ 是由 $H_1$ 和 $H_2$ 生成的子群。（即包含 $H_1$ 和 $H_2$ 的最小子群）。

• $H\vee K=⟨H\cup K⟩$
• $H\wedge K=H\cap K$

格的性质

对偶原理

设 $f$ 是各种元素以及符号 $=,\preccurlyeq ,\succcurlyeq ,\vee ,\wedge$ 的命题，令 $f^{\ast }$ 是 $f$ 的对偶命题，即将 $f$ 中的 $=,\preccurlyeq ,\succcurlyeq ,\vee ,\wedge$ 分别替换为 $\ne ,\succcurlyeq ,\preccurlyeq ,\wedge ,\vee$。

若 $f$ 是真，则 $f^{\ast }$ 也是真。

计算律

• 交换律：
  • $a\vee b=b\vee a$
  • $a\wedge b=b\wedge a$
• 结合律：
  • $(a\vee b)\vee c=a\vee (b\vee c)$
  • $(a\wedge b)\wedge c=a\wedge (b\wedge c)$
• 幂等律：
  • $a\vee a=a$
  • $a\wedge a=a$
• 吸收律：
  • $a\vee (a\wedge b)=a$
  • $a\wedge (a\vee b)=a$

序与运算的关系

若 $L$ 是一个格，$a,b\in L$，则

• $a\preccurlyeq b\iff a\vee b=b\iff a\wedge b=a$
• $a\succcurlyeq b\iff a\vee b=a\iff a\wedge b=b$

保序：即

$$\mathrm{\forall }a,b,c,d\in L,a\preccurlyeq b\wedge c\preccurlyeq d\Rightarrow a\vee c\preccurlyeq b\vee d\mathrm{且}a\wedge c\preccurlyeq b\wedge d$$

一般不满足分配律。

子格

设 $⟨L,\wedge ,\vee ⟩$ 是一个格，$S$ 是 $L$ 的一个非空子集，若 $S$ 关于 $\wedge$ 和 $\vee$ 构成一个格，则称 $⟨S,\wedge ,\vee ⟩$ 是 $⟨L,\wedge ,\vee ⟩$ 的一个子格。

分配格

设 $⟨L,\wedge ,\vee ⟩$ 是一个格，若 $\mathrm{\forall }a,b,c\in L$，满足分配律：

$$\begin{array}{rl}a\wedge (b\vee c)& =(a\wedge b)\vee (a\wedge c)\\ a\vee (b\wedge c)& =(a\vee b)\wedge (a\vee c)\end{array}$$

则称 $⟨L,\wedge ,\vee ⟩$ 是一个分配格。

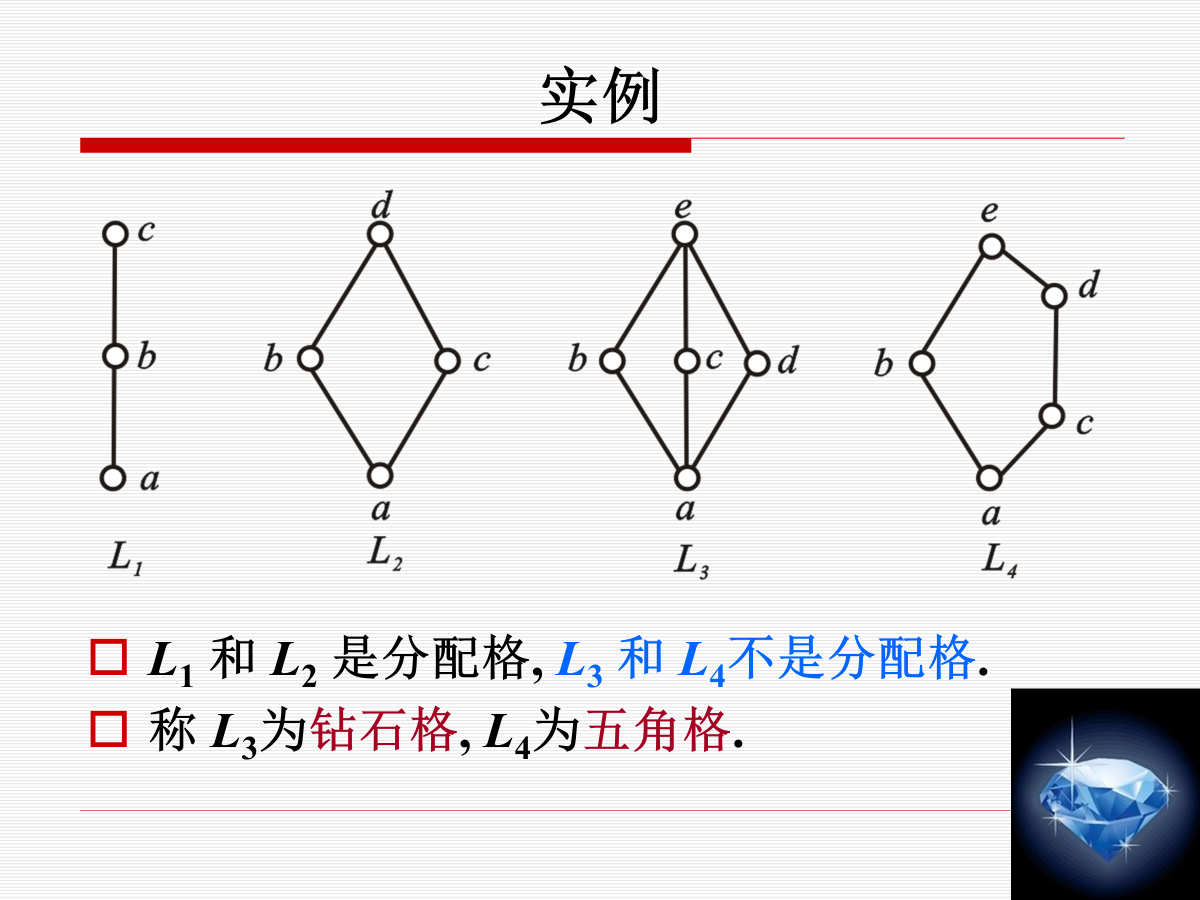
分配格的判定

当且仅当不含与钻石格或五边形格同构的子格。

全上界、全下界

• 若存在 $a\in L$，使得 $\mathrm{\forall }x\in L,x\preccurlyeq a$，则称 $a$ 是 $L$ 的一个全上界。
• 若存在 $b\in L$，使得 $\mathrm{\forall }x\in L,b\preccurlyeq x$，则称 $b$ 是 $L$ 的一个全下界。

$L$ 中的全上界与全下界即为 $L$ 的最大元和最小元。

一般将格 $L$ 的全上界记为 $1$，全下界记为 $0$。 若 $L$ 存在全上界或全下界，则一定是唯一的。

有界格

若 $L$ 存在全上界和全下界，则称 $L$ 是一个有界格。 一般将有界格记为 $⟨L,\wedge ,\vee ,0,1⟩$。 $\mathrm{\forall }a\in L$，有

$$a\vee 0=0,a\vee 1=1,a\wedge 0=0,a\wedge 1=1$$

注意， $\vee$ 和 $\wedge$ 是对偶运算。 $0$ 是 $\wedge$ 的零元，是 $\vee$ 的单位元。 $1$ 是 $\vee$ 的零元，是 $\wedge$ 的单位元。

对于涉及到有界格的命题，如果其中含有全下界 $0$ 或全上界 $1$，在求该命题的对偶命题时，必须将 $0$ 替换成 $1$，而将 $1$ 替换成 $0$。

补元

设 $⟨L,\wedge ,\vee ,0,1⟩$ 是一个有界格，若 $\mathrm{\forall }a\in L$，存在 $a^{\prime }$，使得

$$a\wedge a^{\prime }=0,a\vee a^{\prime }=1$$

则称 $a^{\prime }$ 是 $a$ 的补元。 $a$ 和 $a^{\prime }$ 互为补元。

补元是唯一的。 称任何元素都有补元的有界格为有补格。

布尔代数

如果一个格是有补分配格，则称其为布尔代数，记为 $⟨B,\wedge ,\vee {,}^{\prime },0,1⟩$。

实例：正因子格、幂集格、命题代数、子群格。

有限布尔代数

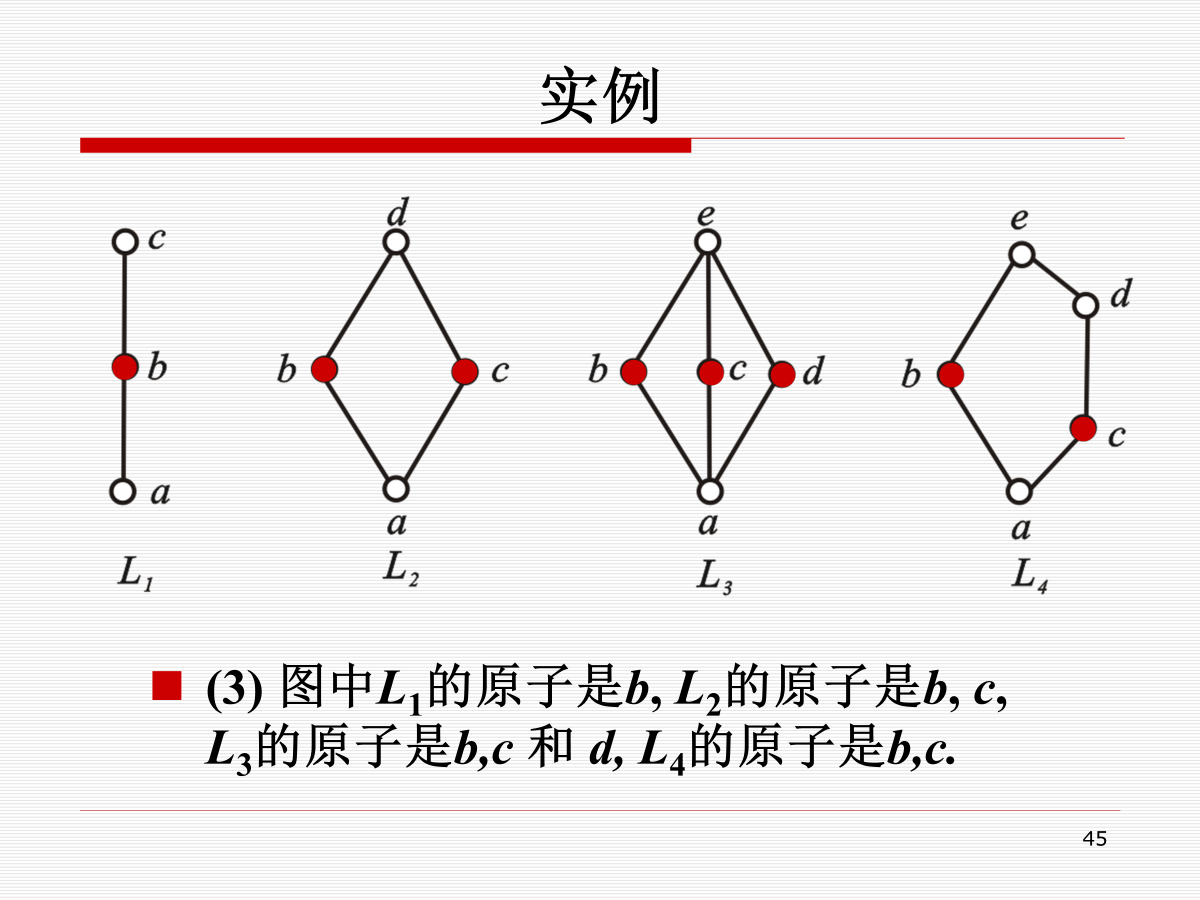
论域 $B$ 为有限集合的布尔代数称为有限布尔代数。 设格 $0\in L$，$L$ 是格， 若 $\mathrm{\exists }a\in L,\mathrm{\forall }x\in L,0\prec x\preccurlyeq a\iff x=a$ 则称 $a$ 是 $L$ 的原子。

设 $A$ 是 有限布尔代数系统 $B$ 的全体原子构成的集合，则 $B$ 同构于 $A$ 的幂集代数 $P(A)$。

推论：

1. 有限布尔代数的基数为 $2^n$。
2. 任何等势的有限布尔代数同构。