图的基本概念

基本概念

无向图

无向图 $G=⟨V,E⟩$，其中：

• $V\ne \varnothing$ 是顶点集，元素称为顶点。
• $E$ 为 $V\mathrm{\&}V$ 的多重子集，其元素称为无向边，简称边。
  • 其中 $\mathrm{\&}$ 表示无序积，即 $A\mathrm{\&}B=\{(a,b)|a\in A\wedge b\in B\}$ 实例：$V=\{v_1,v_2,v_3,v_4,v_5\}$，$E=\{(v_1,v_2),(v_1,v_3),(v_2,v_3),(v_3,v_4),(v_4,v_5)\}$

则 $G=⟨V,E⟩$ 为一无向图。

有向图

有向图 $D=⟨V,E⟩$，其中：

• $V\ne \varnothing$ 是顶点集，元素称为顶点。
• $E$ 为 $V\times V$ 的多重子集，其元素称为有向边。

实例：$V=\{v_1,v_2,v_3,v_4,v_5\}$，$E=\{⟨v_1,v_2⟩,⟨v_1,v_3⟩,⟨v_2,v_3⟩,⟨v_3,v_4⟩,⟨v_4,v_5⟩\}$

相关概念

• 图
  • 可用 $G$ 泛指图（无向图或有向图）
  • $V(G)$，$E(G)$ 分别表示图 $G$ 的顶点集和边集
  • 用 $e_k$ 表示无向边或有向边
  • 用图形表示图时，如果给每一个顶点和每一条边指定一个符号，则称为标定图，否则称为非标定图。
• $n$ 阶图：$|V(G)|=n$
• $n$ 阶零图：$n$ 个顶点，无边
• 平凡图：即 $1$ 阶零图，只有一个顶点且无边
• 空图：$V(G)=\varnothing$

顶点与边的关联关系

• 无向图：

  • 设 $G=⟨V,E⟩$，$e_k=(v_i,v_j)$，则称 $e_k$ 与 $v_i$ 和 $v_j$ 相关联，$v_i$ 和 $v_j$ 称为 $e_k$ 的端点。

  • 若 $v_i\ne v_j$，则称 $e_k$ 与 $v_i$ 和 $v_j$ 的关联次数为 $1$。

  • 若 $v_i=v_j$，则称 $e_k$ 与 $v_i$ 的关联次数为 $2$。并称 $e_k$ 为环。

  • 若 $e_k$ 不与 $v_i$ 相关联，则称 $e_k$ 与 $v_i$ 的关联次数为 $0$。

  • 若 $v_i$ 与 $v_j$ 由边 $e_k$ 相关联，则称 $v_i$ 与 $v_j$ 相邻。

  • 若 $e_i$ 与 $e_j$ 有至少一个公共顶点，则称 $e_i$ 与 $e_j$ 相邻。

• 有向图：
  • 设 $D=⟨V,E⟩$，$e_k=⟨v_i,v_j⟩$，则称 $e_k$ 与 $v_i$ 和 $v_j$ 相关联。$v_i$ 和 $v_j$ 为 $e_k$ 的端点，$v_i$ 为始点，$v_j$ 为终点。
  • 若 $v_i=v_j$，则称 $e_k$ 为 $D$ 中的环。
  • 若 $v_i$ 和 $v_j$ 由边 $e_k$ 相关联，则称 $v_i$ 与 $v_j$ 相邻。
  • 若 $e_i$ 的终点与 $e_j$ 的始点相同，则称 $e_i$ 与 $e_j$ 相邻。
• 图中没有关联的顶点称为孤立点。

顶点的邻域

• 无向图：
  • 邻域：$N_G(v)=\{u|u\in V(G)\wedge \mathrm{\exists }{e}_k=(v,u)\in E(G)\wedge u\ne v\}$
  • 闭邻域：${\bar{N}}_G(v)=N_G(v)\cup \{v\}$
  • 关联集：$I_G(v)=\{e_k|e_k=(v,u)\in E(G)\}$
• 有向图：
  • 后继元集：${\mathrm{\Gamma }}_D^{+}(v)=\{u|u\in V(D)\wedge \mathrm{\exists }{e}_k=⟨v,u⟩\in E(D)\wedge u\ne v\}$
  • 先驱元集：${\mathrm{\Gamma }}_D^{-}(v)=\{u|u\in V(D)\wedge \mathrm{\exists }{e}_k=⟨u,v⟩\in E(D)\wedge u\ne v\}$
  • 邻域：$N_D={\mathrm{\Gamma }}_D^{+}(v)\cup {\mathrm{\Gamma }}_D^{-}(v)$
  • 闭邻域：${\bar{N}}_D(v)=N_D(v)\cup \{v\}$

多重图与简单图

• 平行边：若存在 $e_k=e_0$，则称 $e_k$ 是 平行边。平行边的个数称为重数。
• 多重图：存在平行边的图。
• 简单图：无平行边和环的图。

顶点的度

• 度：$d(v)=|\{e_k|e_k=(v,u)\in E(G)\vee e_k=⟨v,u⟩\in E(D)\vee e_k=⟨u,v⟩\in E(D)\}|$

• 入度：$d^{-}(v)=|\{e_k|e_k=⟨u,v⟩\in E(D)\}|$

• 出度：$d^{+}(v)=|\{e_k|e_k=⟨v,u⟩\in E(D)\}|$

• $d(v)=d^{-}(v)+d^{+}(v)$

• $\mathrm{\Delta }(G)=max\{d(v)|v\in V(G)\}$ 称为图 $G$ 的最大度

• $\delta (G)=min\{d(v)|v\in V(G)\}$ 称为图 $G$ 的最小度

  • 类似的可以定义
  • $\mathrm{\Delta }(D)$ 和 $\delta (D)$
  • ${\mathrm{\Delta }}^{+}(D)$ 和 ${\delta }^{+}(D)$
  • ${\mathrm{\Delta }}^{-}(D)$ 和 ${\delta }^{-}(D)$

握手定理

• 无向图 $G=⟨V,E⟩$，则
  • $\sum _{v\in V}d(v)=2|E|=2m$
• 有向图 $D=⟨V,E⟩$，则
  • $\sum _{v\in V}{d}^{+}(v)=\sum _{v\in V}{d}^{-}(v)=|E|=m$
  • $\sum _{v\in V}d(v)=\sum _{v\in V}(d^{+}(v)+d^{-}(v))=2m$

推论：奇度顶点的个数为偶数。

度数列

$V=\{v_1,v_2,\cdots ,v_n\}$，为无向图 $G$ 的顶点集，称：

• $d(v_1),d(v_2),\cdots ,d(v_n)$ 为图 $G$ 的度数列

$V=\{v_1,v_2,\cdots ,v_n\}$，为有向图 $D$ 的顶点集，称：

• $d^{+}(v_1),d^{+}(v_2),\cdots ,d^{+}(v_n)$ 为图 $D$ 的出度数列
• $d^{-}(v_1),d^{-}(v_2),\cdots ,d^{-}(v_n)$ 为图 $D$ 的入度数列
• $d(v_1),d(v_2),\cdots ,d(v_n)$ 为图 $D$ 的度数列

对于给定的度数列 $d_1,d_2,\cdots ,d_n$，若存在一个 $n$ 阶无向图 $G$，使得 $d(v_1),d(v_2),\cdots ,d(v_n)$ 为 $G$ 的度数列，则称 $d$ 是可图化的。

非负整数序列 $d_1,d_2,\cdots ,d_n$ 是可图化的当且仅当：

$$\sum _{i=1}^n{d}_i=2\mathrm{是}\mathrm{偶}\mathrm{数}$$

对任意 $n$ 阶无向简单图 $G$，满足 $\mathrm{\Delta }(G)\le n-1$ 和 $\delta (G)\ge 0$。

图的同构

若存在双射函数 $f:V_1\to V_2$，使得对于 $v_i,v_j\in V_1$，

$$\begin{array}{rl}(v_i,v_j)\in E_1& \iff (f(v_i),f(v_j))\in E_2\\ ⟨v_i,v_j⟩\in E_1& \iff ⟨f(v_i),f(v_j)⟩\in E_2\end{array}$$

且 $(v_i,v_j)$ 与 $(f(v_i),f(v_j))$ 的重数相同，则称 $G_1$ 与 $G_2$ 同构。 （$⟨v_i,v_j⟩$ 与 $⟨f(v_i),f(v_j)⟩$ 的重数相同） 记作 $G_1\cong G_2$。

图之间的同构关系具有自反性、对称性和传递性。 能找到多条同构的必要条件，但它们全不是充分条件；

• 边数相同；
• 顶点数相同；
• 度数列相同；
  判断两个图同构是个难题

图的分类

完全图与竞赛图

• $n$ 阶无向完全图：$K_n=⟨V,E⟩$，其中 $V=\{v_1,v_2,\cdots ,v_n\}$，$E=\{(v_i,v_j)|1\le i<j\le n\}$
  • ${\displaystyle m=\frac{n(n-1)}{2}}$
  • $\mathrm{\Delta }=\delta =n-1$
• $n$ 阶有向完全图：$K_n^d=⟨V,E⟩$，其中 $V=\{v_1,v_2,\cdots ,v_n\}$，$E=\{⟨v_i,v_j⟩|1\le i\ne j\le n\}$
  • $m=n(n-1)$
  • $\mathrm{\Delta }=\delta =2(n-1)$
  • ${\mathrm{\Delta }}^{+}={\delta }^{+}=n-1$
  • ${\mathrm{\Delta }}^{-}={\delta }^{-}=n-1$
• $n$ 阶无向竞赛图：基图为 $K_n$ 的有向简单图。
  • ${\displaystyle m=\frac{n(n-1)}{2}}$
  • $\mathrm{\Delta }=\delta =n-1$

正则图

设 $G$ 为 $n$ 阶无向简单图，若 $\mathrm{\forall }v\in V(G),d(v)=k$，则称 $G$ 为 $k$ - 正则图。

$$m=\frac{kn}{2}$$

子图

$G=⟨V,E⟩$，$G^{\prime }=⟨V^{\prime },E^{\prime }⟩$

• 子图：$G^{\prime }\subseteq G$，当且仅当 $V^{\prime }\subseteq V$ 且 $E^{\prime }\subseteq E$，称 $G^{\prime }$ 为 $G$ 的子图，$G$ 为 $G^{\prime }$ 的母图。
• 生成子图：$G^{\prime }\subseteq G$ 且 $V^{\prime }=V$，称 $G^{\prime }$ 为 $G$ 的生成子图。
• 真子图：$V^{\prime }⫋V$ 或 $E^{\prime }⫋E$，称 $G^{\prime }$ 为 $G$ 的真子图。
• 导出子图：
  • $V^{\prime }⫋V$ 且 $V^{\prime }\ne \varnothing$，以 $G$ 中两个端点都在 $V^{\prime }$ 中的边组成边集 $E^{\prime }$，称 $G^{\prime }=⟨V^{\prime },E^{\prime }⟩$ 为 $G$ 的 $V^{\prime }$ 导出的子图。记作 $G[V^{\prime }]$。
  • $E^{\prime }⫋E$ 且 $E^{\prime }\ne \varnothing$，以 $G$ 中两个端点都在 $E^{\prime }$ 中的顶点组成顶点集 $V^{\prime }$，称 $G^{\prime }=⟨V^{\prime },E^{\prime }⟩$ 为 $G$ 的 $E^{\prime }$ 导出的子图。记作 $G[E^{\prime }]$。

补图

$G=⟨V,E⟩$，$G^{\prime }=⟨V,E^{\prime }⟩$，其中 $E^{\prime }=\{(v_i,v_j)|v_i,v_j\in V\wedge (v_i,v_j)\notin E\wedge i\ne j\}$，称 $G^{\prime }$ 为 $G$ 的补图。记作 $\bar{G}$。 即添加上 $G$ 中不在 $K_n$ 中的边。

若 $G\cong \bar{G}$，则称 $G$ 为自补图。

删除与增加边与顶点

• 删除边：$G-e_k=⟨V,E-\{e_k\}⟩$
• 删除顶点：$G-v_i=⟨V-\{v_i\},E-\{e_k|e_k=(v_i,v_j)\in E\vee e_k=⟨v_j,v_i⟩\in E\}⟩$
• 边的收缩：从 $G$ 中删除 $e$ 后，将 $e$ 的两个端点合并为一个顶点，得到的图称为 $G$ 的边的收缩。记作 $G\mathrm{\setminus }e$。
• 新加边：$G+e_k=⟨V,E\cup \{e_k\}⟩$

在收缩边和新加边的过程可能会产生平行边和环。

通路与回路

设 $\Gamma$ 为 $G$ 中顶点与边的交替序列，即 $\Gamma =v_0{e}_1{v}_1{e}_2\cdots e_l{v}_l$ 称 $\Gamma$ 为 $G$ 中的通路，$v_0,v_l$ 分别称为 $\Gamma$ 的始点和终点，$l$ 称为 $\Gamma$ 的长度。

• 通路与回路：
  • 若 $v_0=v_l$，则称 $\Gamma$ 为回路。
• 简单通路与简单回路：
  • 所有边互不相同的通路称为简单通路。
  • 所有边互不相同的回路称为简单回路。
• 初级通路（路径）与初级回路（圈）：
  • 顶点互不相同的简单通路称为初级通路。也称为路径。
  • 顶点互不相同的简单回路称为初级回路。也称为圈。
  • 若存在 $v_i$ 到 $v_j$ 的通路，则必定存在长度小于或等于 $n-1$ 的初级通路。
  • 若存在 $v_i$ 回到自身的回路，则必定存在长度小于或等于 $n$ 的初级回路。
• 复杂通路与复杂回路：
  • 有重复边的通路称为复杂通路。
  • 有重复边的回路称为复杂回路。

环 是长度为 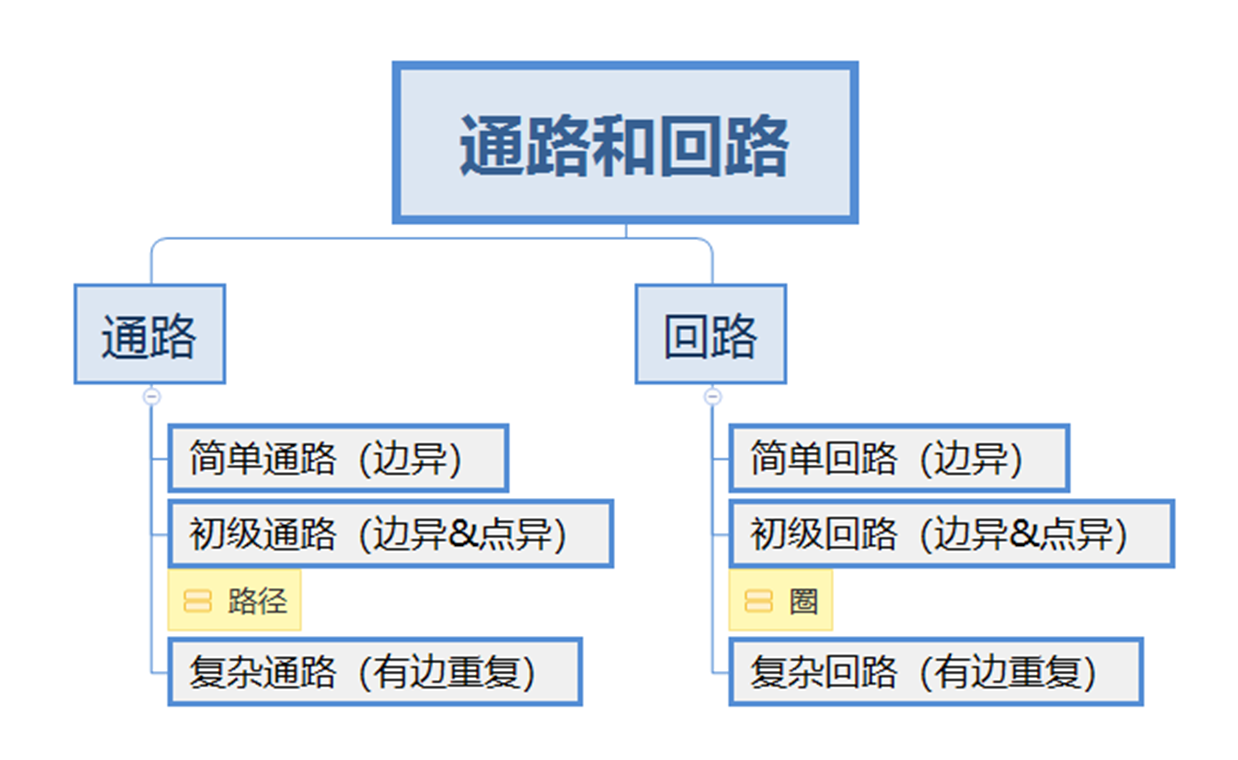$1$ 的圈。

图的连通性

无向图

• 顶点之间的连通关系：$G=⟨V,E⟩$ 为无向图
  • 若 $v_i$ 到 $v_j$ 有通路，则 $v_i\sim v_j$
  • $\sim$ 是 $V$ 上的等价关系
  • 定义 $v_i$ 与自身连通
• $G$ 的连通性与连通分支
  • 连通：若 $\mathrm{\forall }u,v\in V$，$u\sim v$，则称 $G$ 连通
  • 连通分支：$V/R=V_1,V_2,\cdots ,V_k$，$V_i$ 为 $G$ 的连通分支，$k=1$ 时 $G$ 连通。连通分支的个数记为 $p(G)$。

短线程与距离

• 短线程：$v_i$ 到 $v_j$ 的短线程是 $v_i$ 到 $v_j$ 的最短通路
• 距离：$d(u,v)$ 是 $u$ 到 $v$ 的短线程的长度
  • $d(u,v)\ge 0$
  • $u\nsim v\Rightarrow d(u,v)=\mathrm{\infty }$
  • $u=v\Rightarrow d(u,v)=0$
  • $d(u,v)=d(v,u)$
  • $d(u,v)\le d(u,w)+d(w,v)$

割点与割边

$G=⟨V,E⟩$ 为无向图，若存在 $V^{\prime }⫋V$，使得 $p(G-V^{\prime })>p(G)$，且对于任意 $V^{″}⫋V$，$p(G-V^{″})=p(G)$，则称 $V^{\prime }$ 为 $G$ 的点割集。 若 $V^{\prime }=\{v\}$，则称 $v$ 为 $G$ 的割点。

$G=⟨V,E⟩$ 为无向图，若存在 $E^{\prime }⫋E$，使得 $p(G-E^{\prime })>p(G)$，且对于任意 $E^{″}⫋E$，$p(G-E^{″})=p(G)$，则称 $E^{\prime }$ 为 $G$ 的边割集。 若 $E^{\prime }=\{e\}$，则称 $e$ 为 $G$ 的割边或桥。

连通度

设 $G$ 为无向连通图且不是完全图，则称

$$\kappa (G)=min\{|V^{\prime }||V^{\prime }\text{ 是 }G\text{ 的割点集}\}$$

为 $G$ 的点连通度，简称连通度。简记为 $\kappa$。

• 完全图：$\kappa (K_n)=n-1$
• 树：$\kappa (T)=1$
• 非连通图：$\kappa (G)=0$
• k-连通图：$\kappa (G)\ge k$
  • 删除任意 $k-1$ 个顶点后，图仍然连通

称

$$\lambda (G)=min\{|E^{\prime }||E^{\prime }\text{ 是 }G\text{ 的割边集}\}$$

为 $G$ 的边连通度。简记为 $\lambda$。

• 完全图：$\lambda (K_n)=n-1$
• 树：$\lambda (T)=1$
• 非连通图：$\lambda (G)=0$
• r-边连通图：$\lambda (G)\ge r$
  • 删除任意 $r-1$ 条边后，图仍然连通

$$\kappa \le \lambda \le \delta$$

有向图

• 顶点之间的可达关系：$D=⟨V,E⟩$ 为有向图
  • 若 $v_i$ 到 $v_j$ 有通路，则 $v_i$ 可达 $v_j$，记作 $v_i\to v_j$
  • 若 $v_i\to v_j$ 且 $v_j\to v_i$，则称 $v_i$ 与 $v_j$ 相互可达，记作 $v_i\leftrightarrow v_j$
  • 定义 $v_i$ 可达自身
  • $\leftrightarrow$ 是 $V$ 上的等价关系

短线程与距离

距离记作 $d⟨u,v⟩$，定义与无向图相同。 类似无向图的定义，只不过无对称性。

连通图

• 弱连通图：$D$ 的基图是连通图，则称 $D$ 为弱连通图，简称连通图。
• 单向连通图：$\mathrm{\forall }u,v\in V$，$u\to v$ 或 $v\to u$，则称 $D$ 为单向连通图。
• 强连通图：$\mathrm{\forall }u,v\in V$，$u\leftrightarrow v$，则称 $D$ 为强连通图。

强连通 $\Rightarrow$ 单向连通 $\Rightarrow$ 弱连通

• 判定定理：
  • $D$ 单向连通当且仅当 $D$ 中存在经过每个节点至少一次的通路。
  • $D$ 强连通当且仅当 $D$ 中存在经过每个节点至少一次的回路。

图的矩阵表示

关联矩阵

无向图

$(m_{ij}{)}_{n\times m}=v_i\text{ 与 }{e}_j\text{ 相关联的次数}$ 记作 $M(G)=(m_{ij}{)}_{n\times m}$

有向图

$(m_{ij}{)}_{n\times m}=\{\begin{array}{ll}1,& \text{若 }{v}_i\text{ 为 }{e}_j\text{ 的始点}\\ -1,& \text{若 }{v}_i\text{ 为 }{e}_j\text{ 的终点}\\ 0,& \text{其他}\end{array}$

邻接矩阵

$(a_{ij}{)}_{n\times n}=v_i\text{ 到 }{v}_j\text{ 边的条数}$ 记作 $A(D)=(a_{ij}{)}_{n\times n}$

$A_{ij}^l$ 表示 $v_i$ 到 $v_j$ 的长度为 $l$ 的通路的条数。

可达矩阵

$(p_{ij}{)}_{n\times n}=\{\begin{array}{ll}1,& \text{若 }{v}_i\text{ 到 }{v}_j\text{ 可达}\\ 0,& \text{其他}\end{array}$ 记作 $P(D)=(p_{ij}{)}_{n\times n}$

图的运算

$G_1=⟨V_1,E_1⟩$，$G_2=⟨V_2,E_2⟩$

• 若 $V_1\cap V_2=\varnothing$，则称 $G_1$ 和 $G_2$ 是不交的。

• 若 $E_1\cap E_2=\varnothing$，则称 $G_1$ 和 $G_2$ 是边不交的或边不重的。

• 并图：

  • 边集：$E_1\cup E_2$
  • 顶点集：$V_1\cup V_2$
  • 记作 $G_1\cup G_2$

• 交图：

  • 边集：$E_1\cap E_2$
  • 顶点集：$V^{\prime }=\{v|\mathrm{\exists }u,(v,u)\in E_1\cap E_2\vee \mathrm{\exists }u,(u,v)\in E_1\cap E_2\}$
  • 记作 $G_1\cap G_2$

• 差图：

  • 边集：$E_1-E_2$
  • 顶点集：$V^{\prime }=\{v|\mathrm{\exists }u,(v,u)\in E_1-E_2\vee \mathrm{\exists }u,(u,v)\in E_1-E_2\}$
  • 记作 $G_1-G_2$

• 环和图：

  • 边集：$E_1\oplus E_2=(E_1-E_2)\cup (E_2-E_1)$
  • 顶点集：$V^{\prime }=\{v|\mathrm{\exists }u,(v,u)\in E_1\oplus E_2\vee \mathrm{\exists }u,(u,v)\in E_1\oplus E_2\}$
  • 记作 $G_1\oplus G_2$