欧拉图与哈密顿图
欧拉图
- 欧拉通路:经过图中每条边一次且仅一次的通路称为欧拉通路。
- 欧拉回路:经过图中每条边一次且仅一次的回路称为欧拉回路。
- 欧拉图:包含欧拉回路的图称为欧拉图。
- 半欧拉图:包含欧拉通路但不包含欧拉回路的图称为半欧拉图。
规定平凡图是欧拉图。 欧拉通路与欧拉回路是简单通路与简单回路
判定定理
无向图
无向图
有向图
有向图
欧拉图的性质
非环非平凡欧拉图
即
哈密顿图
- 哈密顿通路:经过图中每个顶点一次且仅一次的通路称为哈密顿通路。
- 哈密顿回路:经过图中每个顶点一次且仅一次的回路称为哈密顿回路。
- 哈密顿图:包含哈密顿回路的图称为哈密顿图。
- 半哈密顿图:包含哈密顿通路但不包含哈密顿回路的图称为半哈密顿图。
规定平凡图是哈密顿图。 哈密顿通路与哈密顿回路是初级通路与初级回路。
必要条件
设
其中
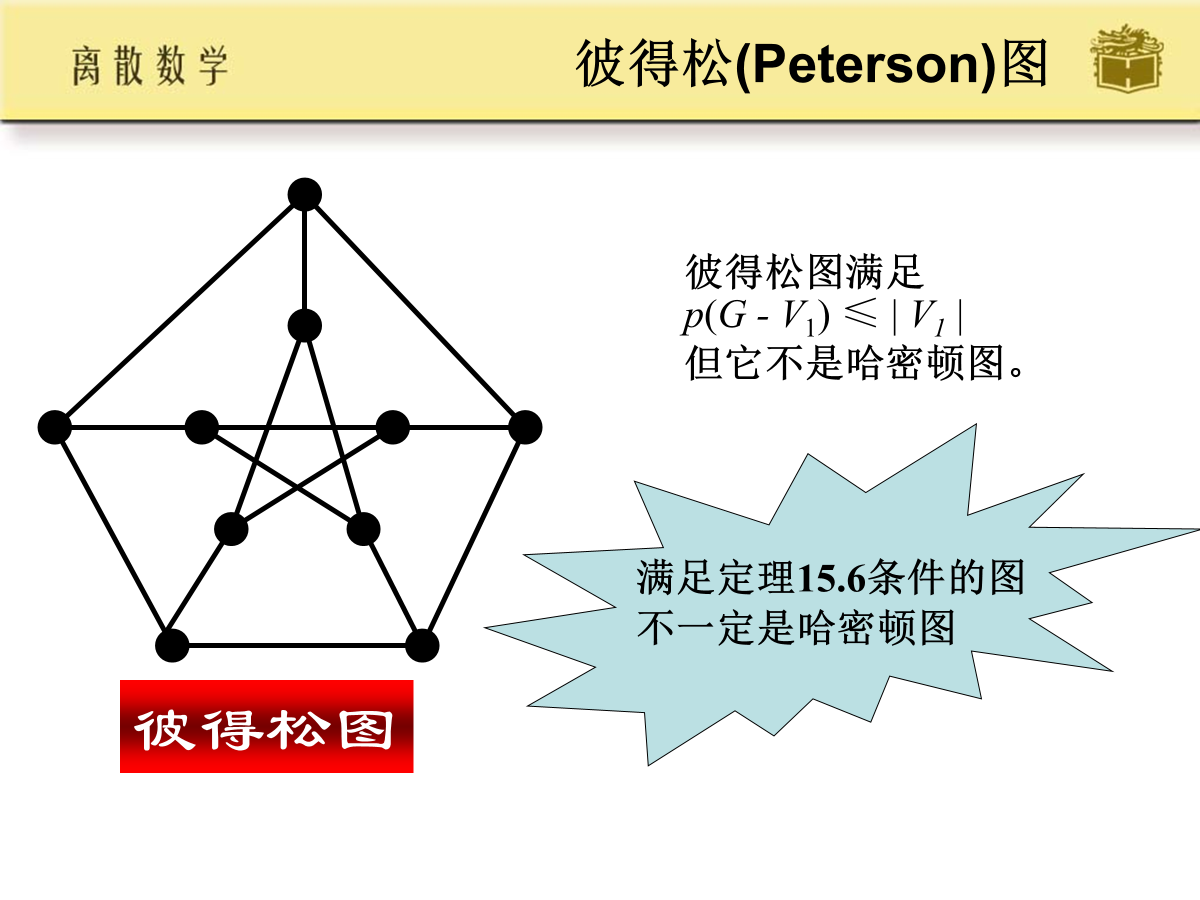
设
充分条件
设
则
若:
则