第五章：关系代数（Relational Algebra）笔记

一、什么是关系代数？

关系代数是一种用于操作关系（表）的数学语言，是数据库查询语言的理论基础。

核心概念：

• 操作对象：关系（即表）
• 操作符：选择、投影、连接、集合运算等
• 目标：用这些操作符构建查询表达式，获取我们需要的数据

---

二、核心操作符（Core Operators）

操作	符号	说明
并（Union）	$\cup$	合并两个关系
交（Intersection）	$\cap$	取两个关系共有的元组
差（Difference）	$-$	取第一个中有但第二个中没有的元组
选择（Selection）	${\sigma }_C$	筛选满足条件的行
投影（Projection）	$\pi$	选出指定列，并去重
广义投影（Extended Projection）	$\pi$	可以进行计算、重命名
笛卡尔积（Product）	$\times$	将两个表的所有行组合起来
Theta 连接（Theta Join）	${\bowtie }_C$	基于条件$C$的连接（如$A=B$）
自然连接（Natural Join）	$\bowtie$	自动按同名属性等值连接，去掉重复列
重命名（Renaming）	$\rho$	给关系或属性起新名字
去重（Duplicate Elimination）	$\delta$	去重，将重复元组合并为一条
排序（Sorting）	$\tau$	按指定属性排序
分组（Grouping）	${\gamma }_L$	按指定属性分组

---

三、详细讲解每个操作符

1. 选择（${\sigma }_C$）

从一个关系中选出满足条件$C$的元组（行）

示例：

$$JoeMenu:={\sigma }_{bar="Jo{e}^{\prime }s"}(Sells)$$

表示从 Sells 表中选出 bar = "Joe's" 的所有记录。

---

2. 投影（$\pi$）

从一个关系中选出某些列（属性），并去除重复元组

示例：

$$Prices:={\pi }_{beer,price}(Sells)$$

从 Sells 表中选出 beer 和 price 列，并去重。

---

3. 广义投影（Extended Projection）

在投影时可以添加新的列，比如通过计算生成新列，也可以对已有列重命名

示例：

设关系$R(A,B)$为：

$$\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$$

广义投影：

$${\pi }_{A+B\to C,A,A}(R)$$

结果为：

$$\left[\begin{array}{ccc}C& A_1& A_2\\ 3& 1& 1\\ 7& 3& 3\end{array}\right]$$

---

4. 笛卡尔积（$\times$）

将两个关系的所有元组进行配对，形成一个新的关系

示例：

$$R3:=R1\times R2$$

注意：如果两个表有相同属性名，需要加前缀区分，如 R1.A, R2.A

---

5. Theta 连接（${\bowtie }_C$）

先做笛卡尔积，再根据某个条件筛选出符合条件的元组

示例：

$$BarInfo:=Sells{\bowtie }_{Sells.bar=Bars.name}Bars$$

相当于先做乘积，再选 bar 相同的记录。

---

6. 自然连接（$\bowtie$）

自动按照相同名称的属性进行等值连接，并自动去掉重复列

示例：

$$BarInfo:=Sells\bowtie Bars$$

系统会自动按 bar 字段连接，并只保留一份 bar 列。

---

7. 重命名（$\rho$）

给关系或属性起新名字，常用于避免列名冲突

示例：

$${\rho }_R(bar,addr)(Bars)$$

将 Bars(name, addr) 重命名为 R(bar, addr)

8. 去重（$\delta$）

去重，将重复元组合并为一条

9. 排序（${\tau }_L$）

按指定属性排序 $L$ 是排序的属性列表，默认升序

---

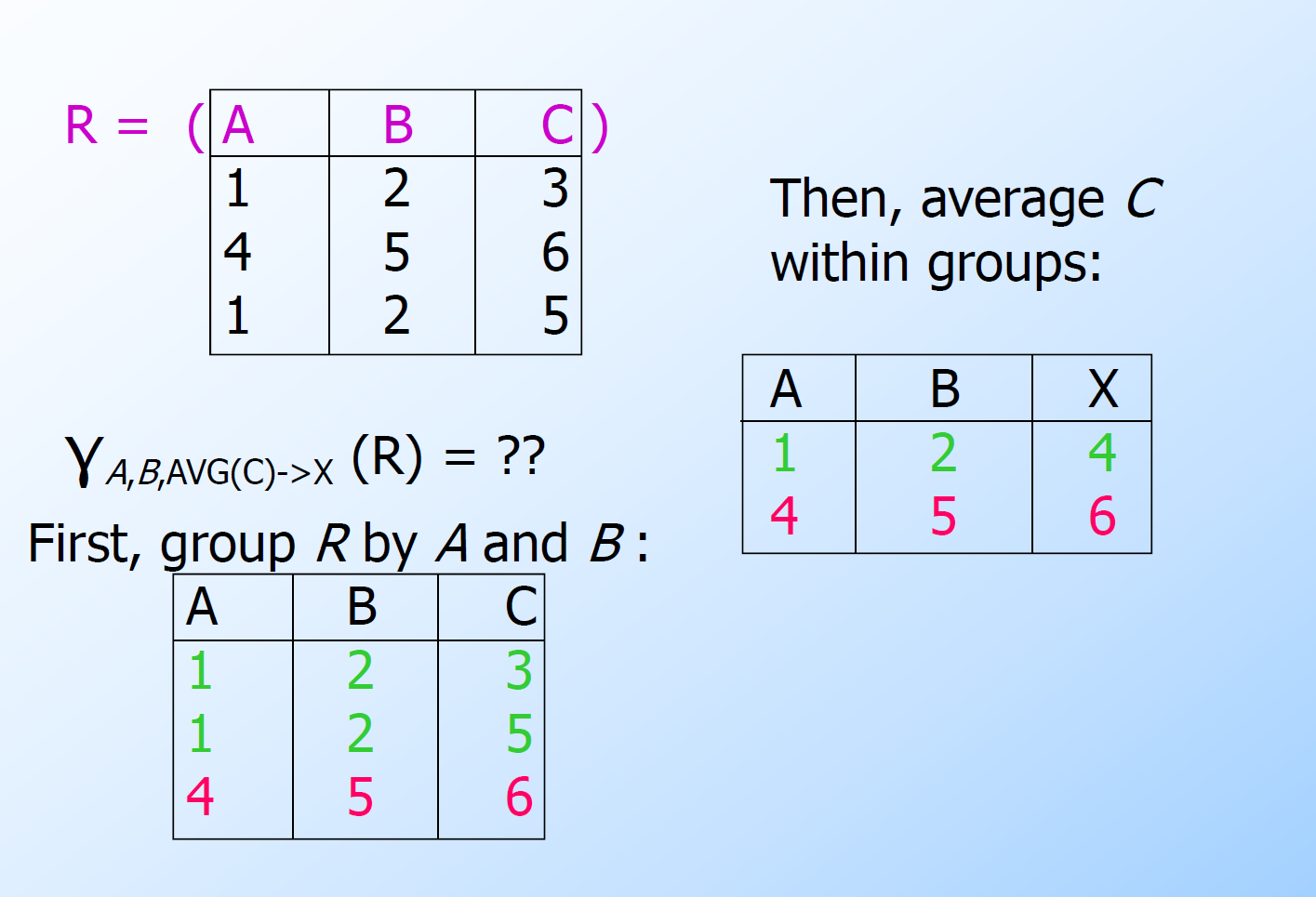
四、构建复杂表达式的方法

1. 使用赋值语句

$$\begin{gathered} R4:=R1\times R2 \\ R3:={\sigma }_C(R4) \end{gathered}$$

2. 嵌套表达式

$$R3:={\sigma }_C(R1\times R2)$$

3. 表达式树（Expression Tree）

图形化表示查询流程，根节点是最终结果，子节点是输入和操作。

示例：

       ∪
      / \
 πname   πbar
    |       |
 σaddr=“Maple St.”   σprice<3 AND beer=“Bud”
    |                   |
  Bars               Sells

---

五、结果模式（Schema of Results）

操作	结果模式
并、交、差	同两个操作数的模式
选择	与原表结构相同
投影	指定列组成的结构
笛卡尔积	所有属性合并，若重名则加前缀
Theta 连接	同笛卡尔积
自然连接	合并两个表的属性，去掉重复列
重命名	按照重命名规则来定义

---

六、多包代数（Bag Algebra）

SQL 实际上是一种基于“包”（bag 或 multiset）的语言，即允许重复元组存在。

包 vs 集合

操作	包的行为	集合的行为
选择（$\sigma$）	对每一行单独处理，不影响重复性	同左
投影（$\pi$）	不去重	去重
并（$\cup$）	求和（如$\{1\}\cup \{1\}=\{1,1\}$）	合并（$\{1\}\cup \{1\}=\{1\}$）
交（$\cap$）	取最小出现次数	同集合
差（$-$）	出现次数相减（不能为负）	同集合

---

七、关系代数定律（Algebra Laws）

一些在集合代数中成立的定律在包代数中不一定成立：

定律	是否适用于包？
并交换律（$R\cup S=S\cup R$）	✅ 成立
并幂等律（$R\cup R=R$）	❌ 不成立（包中变成两倍）
连接结合律	✅ 成立
分配律	❌ 不一定成立

---

八、总结表格

操作符	中文名	功能
$\sigma$	选择	选出满足条件的行
$\pi$	投影	选出某些列
$\times$	笛卡尔积	两表所有行组合
${\bowtie }_C$	Theta 连接	按条件连接
$\bowtie$	自然连接	按同名属性等值连接
$\rho$	重命名	更改关系或属性名
$\cup$	并	合并两个关系
$\cap$	交	取两个关系共有的元组
$-$	差	取第一个中有但第二个中没有的元组

---

九、典型应用示例

示例 1：查找住在 Maple St 的酒吧名字

$${\pi }_{name}({\sigma }_{addr="MapleSt."}(Bars))$$

示例 2：查找卖 Bud 啤酒价格低于$3 的酒吧

$${\pi }_{bar}({\sigma }_{beer="Bud"\wedge price<3}(Sells))$$

示例 3：查找既在 Maple St 上又卖 Bud 的酒吧（并集）

$${\pi }_{name}({\sigma }_{addr="MapleSt."}(Bars))\cup {\pi }_{bar}({\sigma }_{beer="Bud"\wedge price<3}(Sells))$$

---

如果你需要我帮你整理成 PDF、Word 文档，或者想看图解、练习题，都可以告诉我 😊