多维随机变量及其分布

二维随机变量及其联合分布

分布函数和密度函数

$$F(x,y)=P\{X\le x,Y\le y\}$$$$F(x,y)={\int }_{-\mathrm{\infty }}^x{\int }_{-\mathrm{\infty }}^{y}f(u,v)dudv$$$$\frac{{\partial }^{2}F(x,y)}{\partial x\partial y}=f(x,y)$$

1. 二维均匀分布

$$f(x,y)=\{\begin{array}{ll}\frac{1}{S},& (x,y)\in D\\ 0,& \text{其他}\end{array}$$

2. 二维正态分布

若$(X,Y)$的联合密度函数为

$$f(x,y)=\frac{1}{2\pi {\sigma }_1{\sigma }_2\sqrt{1-{\rho }^2}}{e}^{-\frac{1}{2(1-{\rho }^2)}(\frac{(x-{\mu }_1{)}^2}{{\sigma }_1^2}-\frac{2\rho (x-{\mu }_1)(y-{\mu }_2)}{{\sigma }_1{\sigma }_2}+\frac{(y-{\mu }_2{)}^2}{{\sigma }_2^2})}$$

称$(X,Y)$服从二维正态分布，记为$(X,Y)\sim N({\mu }_1,{\sigma }_1^2,{\mu }_2,{\sigma }_2^2,\rho )$

$\rho$: 相关系数，与下文提到的相关系数相同，都是用来衡量两个变量之间的线性相关性的指标

$$\rho =\frac{Cov(X,Y)}{\sqrt{D(X)D(Y)}}$$

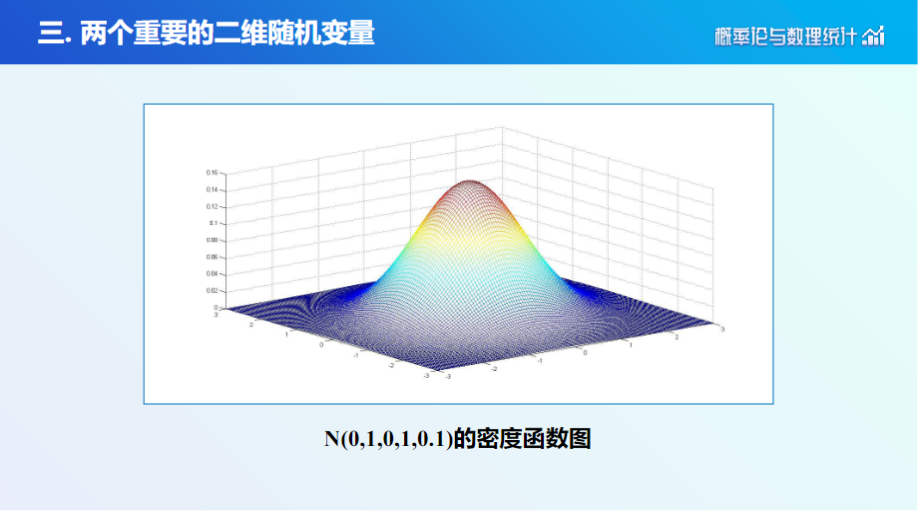
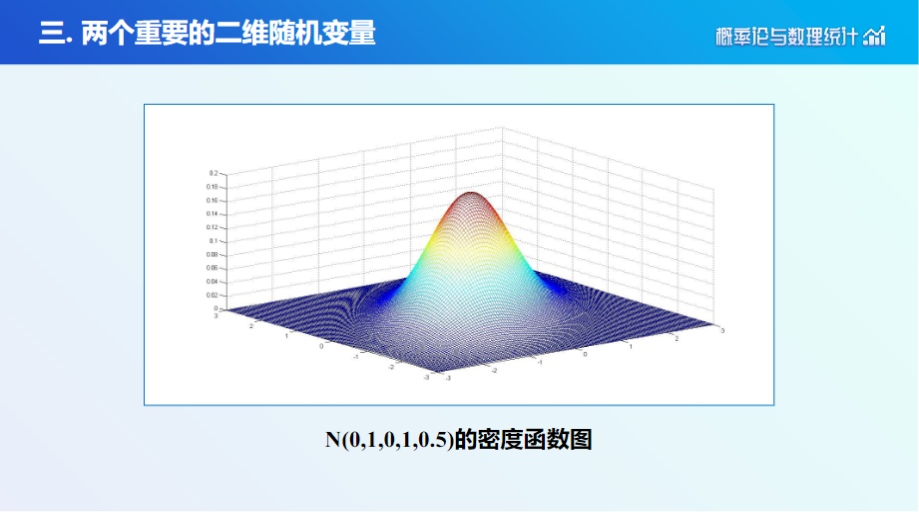
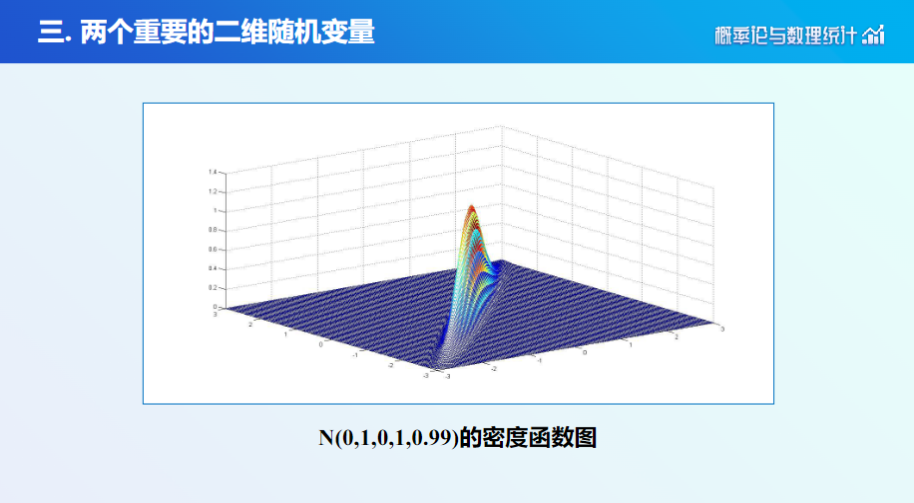
二维随机变量注意点

判定连续型随机变量的本质

不论是一维还是二维情形，在定义连续型随机变量时，其实质在于 它的概率密度函数是否存在，至于它是否可以在一个区间或区域上连续取值不是本质的

两个连续型随机变量不一定构成二维连续型变量

根据二维离散型随机变量的定义，可以认为，如果X和Y都是一维离 散型随机变量，则$(X,Y)$就是二维离散型随机变量

但是对于二维连续型随机变量类似的结论不成立 即，不能说分量X和Y都是一维连续型随机变量则$(X,Y)$就是二维连续型变量。 例如：$Y=X^2$时，$(X,Y)$不构成二维随机变量，因为他们只在一条曲线上而非一个区域内 除了完全相关的情况外，部分相关性或奇异分布等情况也可能导致 $(X,Y)$不具有联合密度函数，从而不能成为二维连续型随机变量。

边缘分布

$$F_X\left(x\right)=F(x,+\mathrm{\infty })=\underset{y\to +\mathrm{\infty }}{lim}F(x,y)$$$$F_Y\left(y\right)=F(+\mathrm{\infty },y)=\underset{x\to +\mathrm{\infty }}{lim}F(x,y)$$$$P\{X=x_i\}=\sum _{i=1}^{\mathrm{\infty }}{p}_{ij}\stackrel{\mathrm{△}}{=}{p}_{i\cdot }$$$$P\{Y=y_i\}=\sum _{i=1}^{\mathrm{\infty }}{p}_{ij}\stackrel{\mathrm{△}}{=}{p}_{\cdot j}$$

$$f_X\left(x\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x,y)dy$$$$f_Y\left(y\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x,y)dx$$

由联合分布可以唯一确定边缘分布，但反之，不一定成立。 二维正态分布$(X,Y)$的边缘分布是一维正态分布。 对这个现象的解释是：边缘概率密度只考虑了单个分量的情况，而未涉及$X$与$Y$之间的关系。

独立性

那么，当$X$和$Y$之间没有任何关系的时候，自然就可以认为由边缘分布能够唯一确定联合分布，这时，称$X$和$Y$是相互独立。

两事件A, B独立的定义是：若$P(AB)=P(A)P(B)$，则称事件A, B独立。将事件独立性推广到随机变量。

随机变量的独立性

设二维随机变量$(X,Y)$的联合分布函数为$F(x,y)$，$F_X(x)$和$F_Y(y)$分别为其边缘分布函数，若对于任意实数$x,y$，有

$$F(x,y)=F_X(x)F_Y(y)$$

则称随机变量$X$和$Y$相互独立，简称$X$和$Y$独立。 当利用独立性的定义判断两个随机变量不独立时，只需证明存在一对实数 $x_0,y_0$， 使得 $F(x_0,y_0)\ne F_X(x_0)F_Y(y_0)$。 若二维随机变量$(X,Y)$相互独立，则有如下结论：

$$P\{a<X\le b,c<Y\le d\}=P\{a<X\le b\}P\{c<Y\le d\}$$$$P\{X>a,Y>b\}=P\{X>a\}P\{Y>b\}$$

离散型随机变量的独立性

若 $(X,Y)$ 为二维离散型随机变量，且其联合分布律为 $P\{X=x_i,Y=y_j\}=p_{ij}$

则 $X$ 和 $Y$ 相互独立的充分必要条件是： 对任意的 $x_i,y_j$，都有 $P\{X=x_i,Y=y_j\}=P\{X=x_i\}P\{Y=y_j\}$。

由此定理可知，当$X$与$Y$独立时，由边缘分布律可以唯一确定联合分布律。 同时，只要存在某个数对 $(x_i,y_j)$ 使得：

$$P\{X=x_i,Y=y_j\}\ne P\{X=x_i\}P\{Y=y_j\}$$

则可以判定X与Y不独立。

连续型随机变量的独立性

若 $(X,Y)$ 为二维连续型随机变量，联合密度函数为 $f(x,y)$，则 $X$, $Y$ 相互独立的充分必要条件是对任意的实数 $x$ 和 $y$，有

$$f(x,y)=f_X(x)f_Y(y)$$

推广到n维随机变量

若对所有的$x_1,x_2,\dots ,x_n$有：

$$F(x_1,x_2,\dots ,x_n)=F_{X_1}(x_1)F_{X_2}(x_2)\dots F_{X_n}(x_n)$$

则称$X_1,X_2,\dots ,X_n$是相互独立的

二维变量函数的分布

二维离散型变量函数的分布

设 $(X,Y)$ 是二维随机变量，$z=g(x,y)$ 是一个已知的二元函数，如果当 $(X,Y)$ 取值为 $(x,y)$ 时，随机变量 $Z$ 取值为 $z=g(x,y)$ ，则称 $Z$ 是二维随机变量 $(X,Y)$ 的函数，记作 $Z=g(X,Y)$ 。

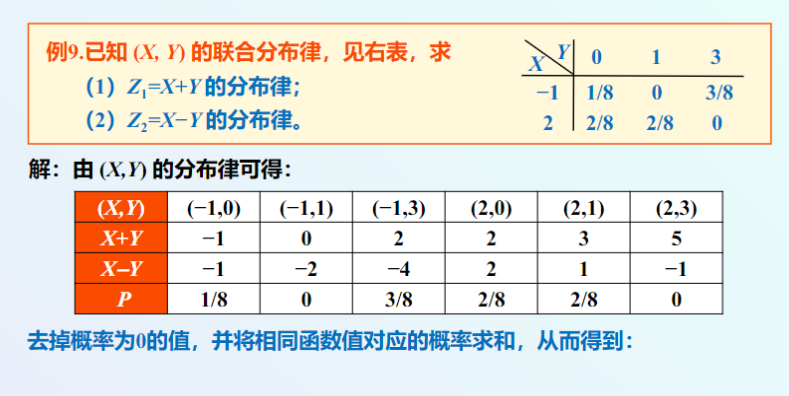
泊松分布具有可加性

$X\sim \pi ({\lambda }_1)$, $Y\sim \pi ({\lambda }_2)$, $X$和$Y$相互独立，则$X+Y\sim \pi ({\lambda }_1+{\lambda }_2)$

二项分布具有可加性

$X\sim b(n_1,p)$, $Y\sim b(n_2,p)$, $X$和$Y$相互独立，则$X+Y\sim b(n_1+n_2,p)$

二维连续型变量函数的分布

设$(X,Y)$是连续型随机变量，其概率密度函数为$f(x,y)$，$Z=g(X,Y)$是$(X,Y)$的函数，一般可以分为以下两种情况讨论。

第一，$Z=g(X,Y)$为离散型随机变量，此时，只需求$Z$的分布律，问题的实质是将$Z$取某个值$z$的概率转化为$(X,Y)$属于某个区域$D$的概率，即有

$$P\{Z=z\}=P\{(X,Y)\in D\}=\int {\int }_{D}f(x,y)dxdy$$

第二，当$Z$不是离散型随机变量时，采用分布函数法求$Z=g(X,Y)$的分布函数

$$F_Z(z)=P\{Z\le z\}=P\{g(X,Y)\le z\}=\int {\int }_{D}f(x,y)dxdy$$

当$Z$为连续型随机变量时，其概率密度函数为

$$f_Z(z)=\frac{d}{dz}{F}_Z(z)$$

瑞利分布

最大值和最小值的分布函数

随机变量 $X$ 和 $Y$ 相互独立，其分布函数分别为 $F_X(x)$ 和 $F_Y(y)$ ，现在来求 $M=max(X,Y)$ 以及 $N=min(X,Y)$ 的分布函数。 设 $M$ 的分布函数为 $F_M(z)$ 。

$$F_M(z)=P\{M\le z\}=P\{X\le z,Y\le z\}$$

由于 $X$ 和 $Y$ 相互独立，于是 $M=max(X,Y)$ 的分布函数为：

$$F_M(z)=P\{X\le z\}P\{Y\le z\}=F_X(z)F_Y(z)$$

即有：

$$F_M(z)=F_X(z)F_Y(z)$$$$F_N(z)=1-[1-F_X(z)][1-F_Y(z)]=1-P\{X>z,Y>z\}$$$$F_N(z)=P\{N\le z\}=1-P\{N>z\}$$

类似的，可求得 $N=min(X,Y)$ 的分布函数 由于 $X$ 和 $Y$ 相互独立，于是 $N=min(X,Y)$ 的分布函数为：

$$F_N(z)=1-P\{X>z\}P\{Y>z\}$$