数理统计学的基本概念
总体与样本
总体
在数理统计学中,把研究对象的全体称为总体(母体),组成总体的每个元素称为个体。 在许多实际问题中,我们关心的不是个体本身,而是个体的某项数量指标,我们将这个数量指标取值的全体称为总体。
样本
从总体中抽取
简单随机样本
如果
- 每个
都与总体 有相同的分布 相互独立
则称
统计量
定义
设
注意:
- 统计量是不含未知参数的样本的函数。
- 统计量既然依赖于样本,而后者又是随机变量,即统计量是随机变量的函数,故统计量是随机变量。
常用统计量
- 样本均值
反应了总体均值
- 样本方差
反应了总体方差
- 样本标准差
反应了总体标准差
- 样本
阶(原点)矩
反应了总体
- 样本
阶中心矩
反应了总体
- 顺序统计量 设
是来自总体 的样本,将 按照从小到大排列为
其中
抽样分布
定义
设
三大抽样分布
chi-square分布
定义
设
满足自由度为
概率密度函数
当
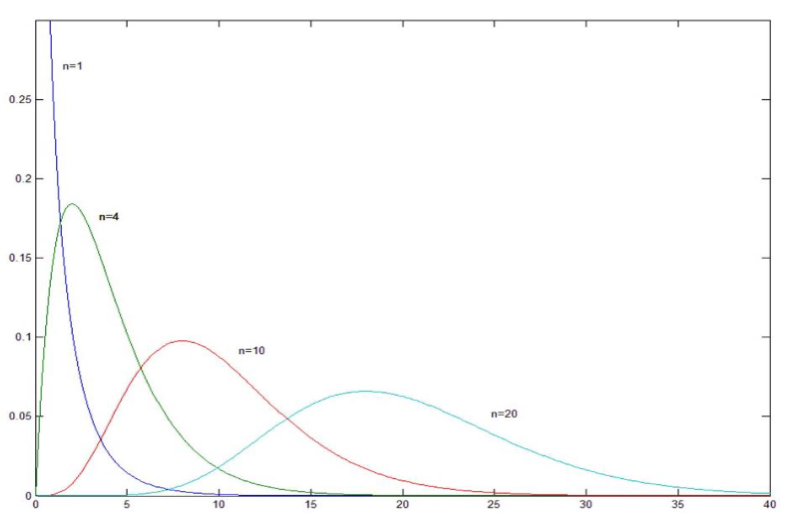
性质
- 设
相互独立,且满足正态分布 ,则:
- 设
,则 , , ,且 与 相互独立,则 ,称为 分布的可加性。

student's t分布
定义
设
满足自由度为
概率密度函数
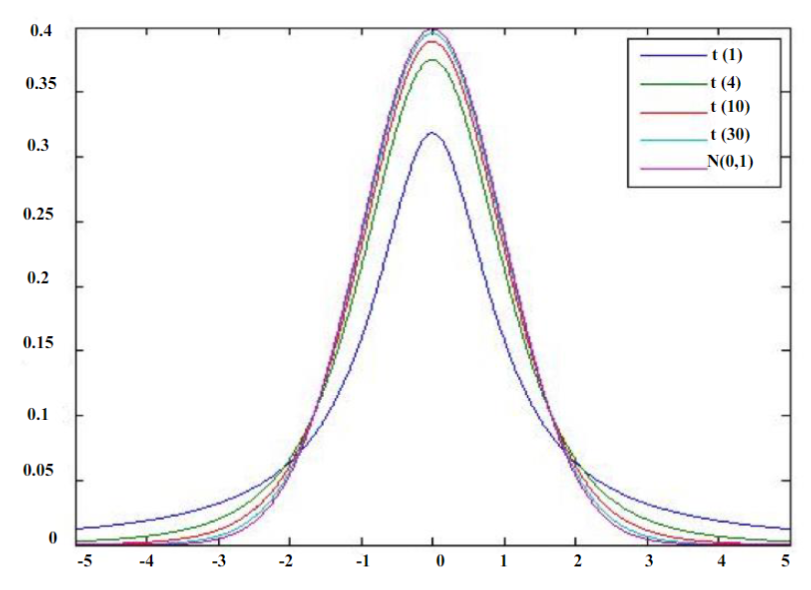
性质
分布的密度函数是关于 对称的。且 。 分布的密度函数形状是中间高,两边低,左右对称,与标准正态分布的概率密度函数图像类似,
即
- 设
, ,则对于 , 存在,且:
- 当
时, 分布即为 分布,即:
其数学期望和方差均不存在。
Fisher分布
定义
设
满足自由度为
概率密度函数
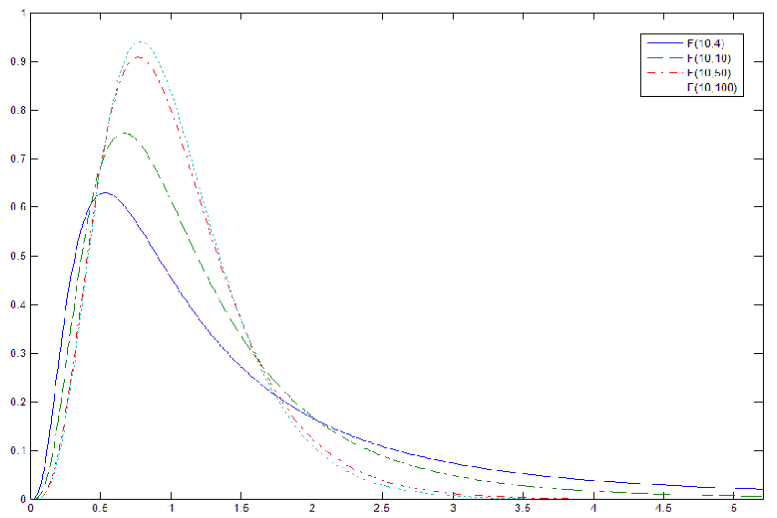
性质
- 设
,则 - 设
,则

要求随机变量独立!
几个重要的抽样分布
引理
设
有:
结论
- 若
是来自正态总体 的样本, 代表样本均值则有
即
- 若
是来自正态总体 的样本, 代表样本方差则有
且
- 若
是来自正态总体 的样本, 与 分别代表样本均值与样本方差,则有
- 若
是来自正态总体 的样本, 是来自正态总体 的样本,且两个样本相互独立, 与 分别代表第一个样本的样本均值与样本方差, 与 分别代表第二个样本的样本均值与样本方差,则有
其中
称为合并方差
- 若
是来自正态总体 的样本, 是来自正态总体 的样本,且两个样本相互独立, 与 分别代表第一个样本的样本均值与样本方差, 与 分别代表第二个样本的样本均值与样本方差,则有